【技术篇】transformer解析

在特征提取中，最早我们使用DNN进行特征提取，这种全连接的方式，虽然可以提取出很多特征，但是这种设计往往只能提取简单特征和整体特征；后来，在图像领域，我们使用了卷积神经网络（CNN），这种依托卷积核的设计，可以让模型提取到图片局部特征。后来，随着深度学习在自然语言处理领域的应用，人们迫切需要设计一种可以结合上下文的特征提取模型，RNN随即出现，它使用了一种串行的时间步的设计，模型提取特征时会结合上一个时间步的特征，这种设计可以让模型提取到序列特征，接着，LSTM和GRU出现，它们在RNN的基础上，增加了记忆单元，可以让模型更好地提取到长期依赖的特征，然而他们具有梯度消失的问题，为了解决这个问题，transformer出现了，它使用了并行计算的自注意力机制，可以让模型更好地提取到结合上下文的特征。

transformer的成功，让人们对于深度学习的特征提取模型有了新的认识，它的出现，不仅仅是为了解决梯度消失的问题，更是为了让模型更好地提取到结合上下文和注意力的特征，这种设计，让transformer在自然语言处理领域有了很好的应用，更在图像处理和时间信号处理领域有了很好的应用。ViT和swin-transformer是transformer在图像领域的应用。

⭐总体概述

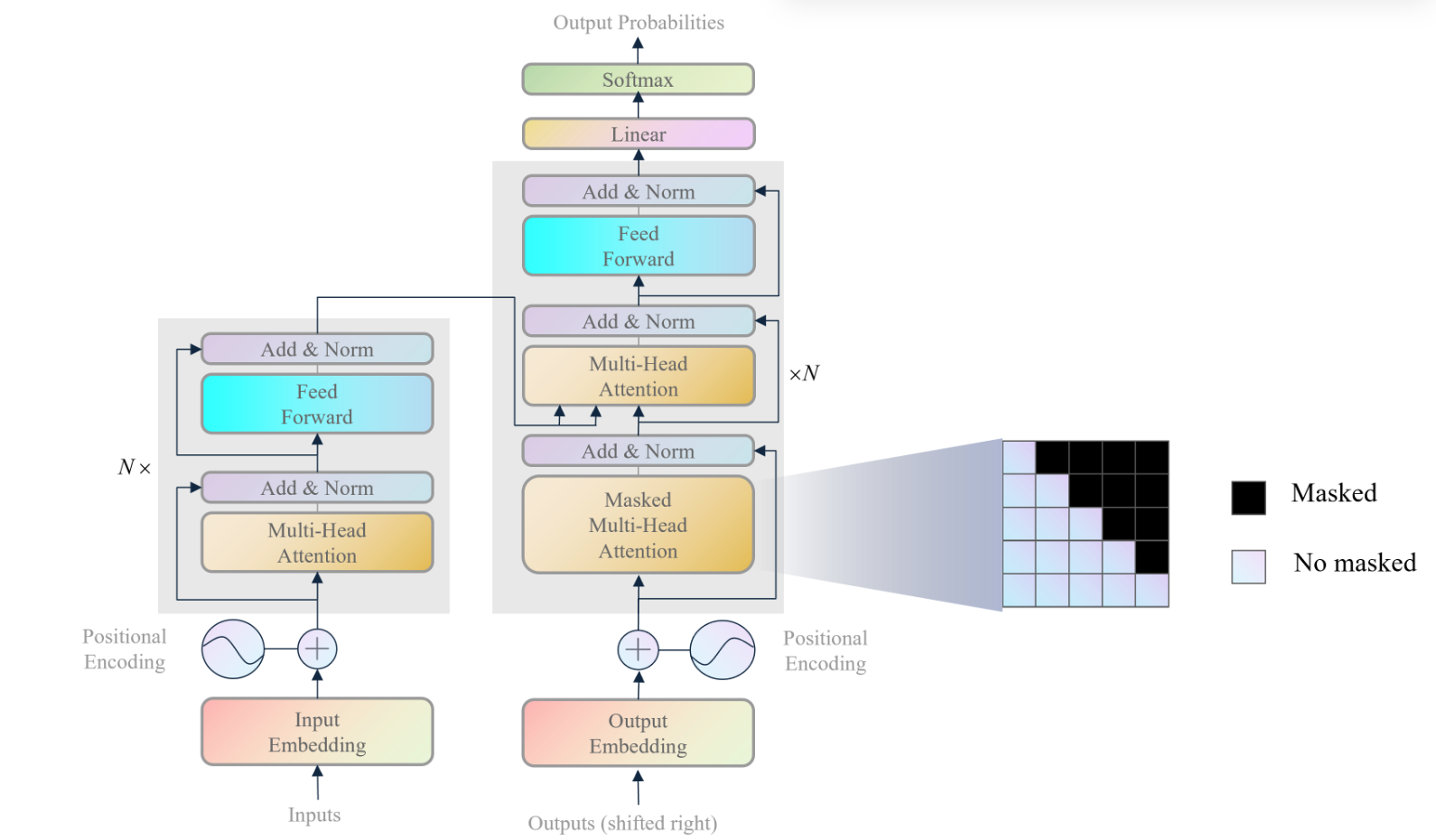
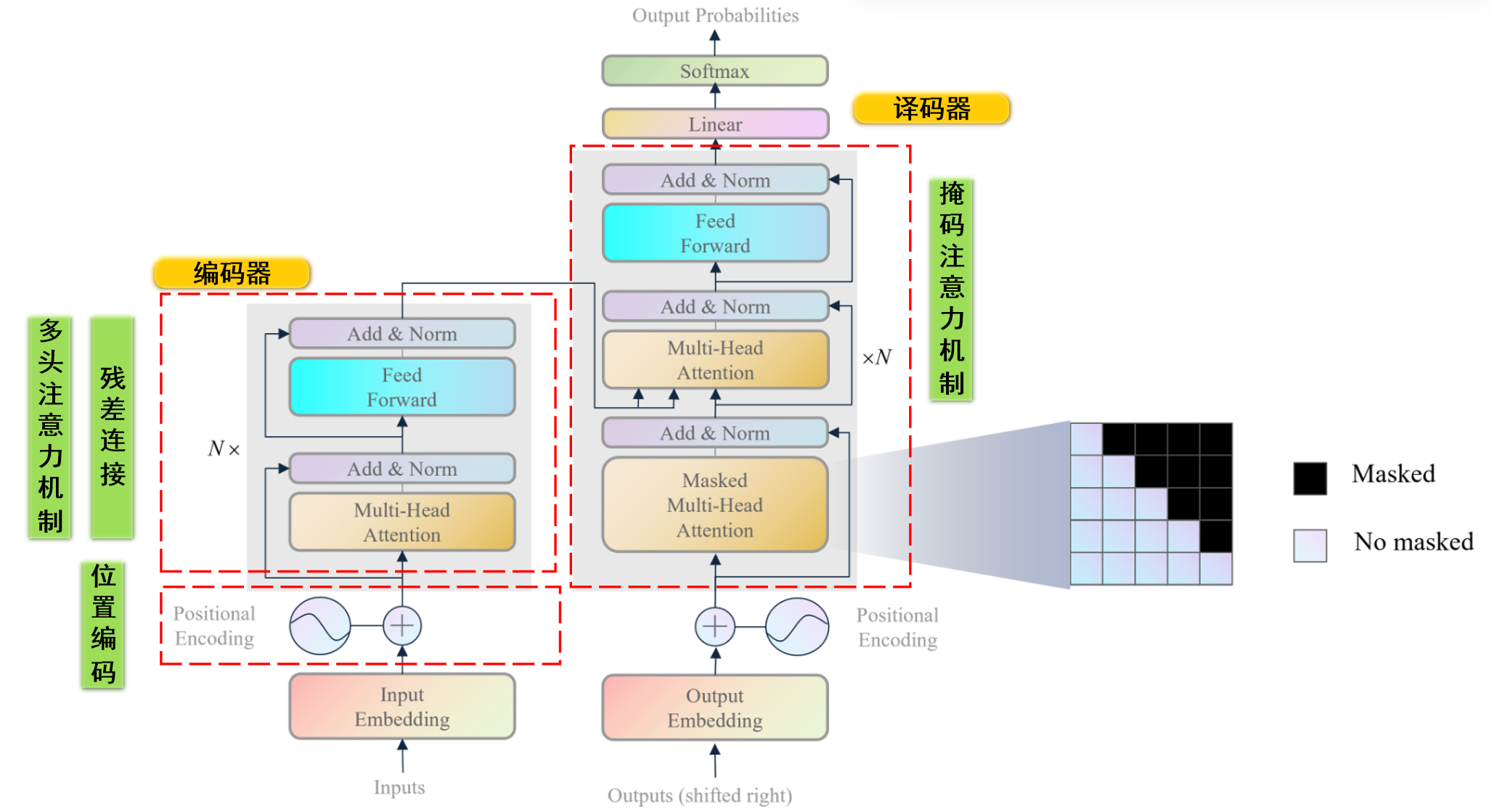
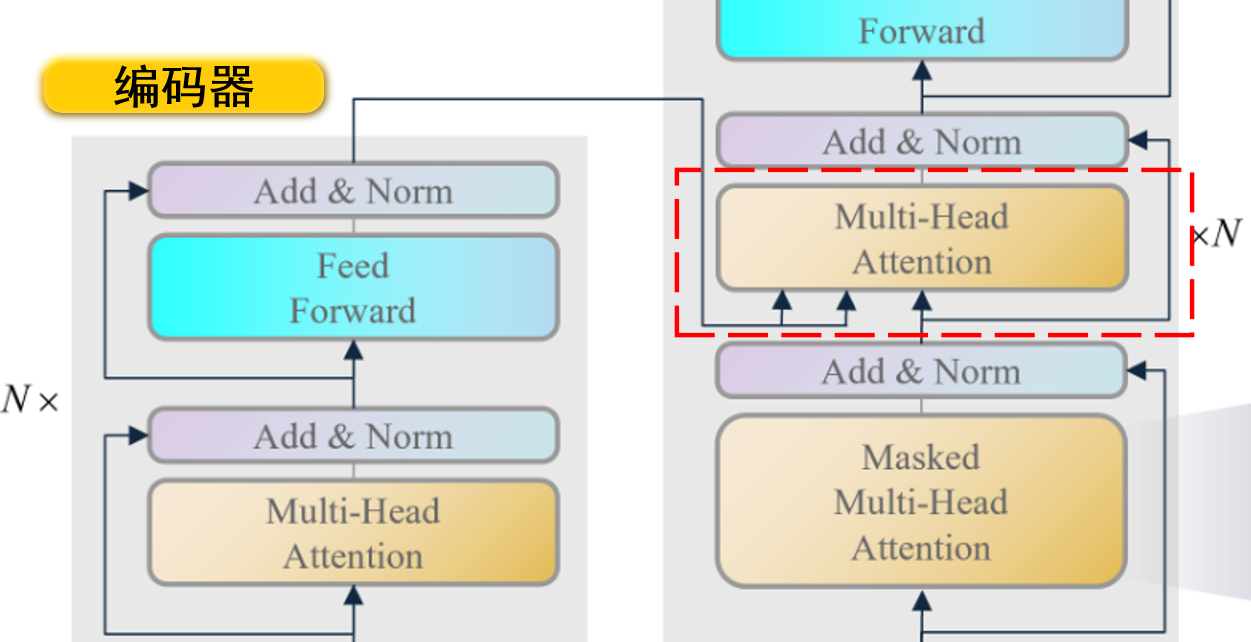
transformer主要由编码器和解码器组成，它具有俩个输入端口，一个是编码器的输入端口，一个是解码器的输入端口，编码器和解码器之间有一个注意力机制，这个注意力机制可以让模型更好地提取到结合上下文的特征。
在训练阶段我们以中译英功能进行示例描述：transformer的第一个输入是原始序列（中文句子），第二个输入是目标序列（英文句子），模型的输出是预测目标序列，模型的训练目标是让模型的输出和目标序列尽可能地接近。
在推理阶段我们以中译英功能继续示例描述：transformer的第一个输入是原始序列（中文句子），第二个输入是目标序列（英文句子），由于推理阶段我们不知道目标序列，所以我们将目标序列设置为start标识符，模型的输出是预测目标序列的第一个单词，然后我们预测的第一个单词拼接start标识符再作为模型的输入，模型的输出是预测目标序列的第二个单词，以此类推，直到模型的输出是结束符号为止。注意，接下来，如果非特殊说明，笔者只针对训练阶段进行介绍，且以中译英任务为例。

• 编码器功能：transformer的编码器是为了提取原始序列的上下文特征，供解码器参考上下文信息。
• 译码器功能：transformer的解码器是为了结合原始序列的上下文特征和掩盖后目标序列的特征，预测完整的目标序列。

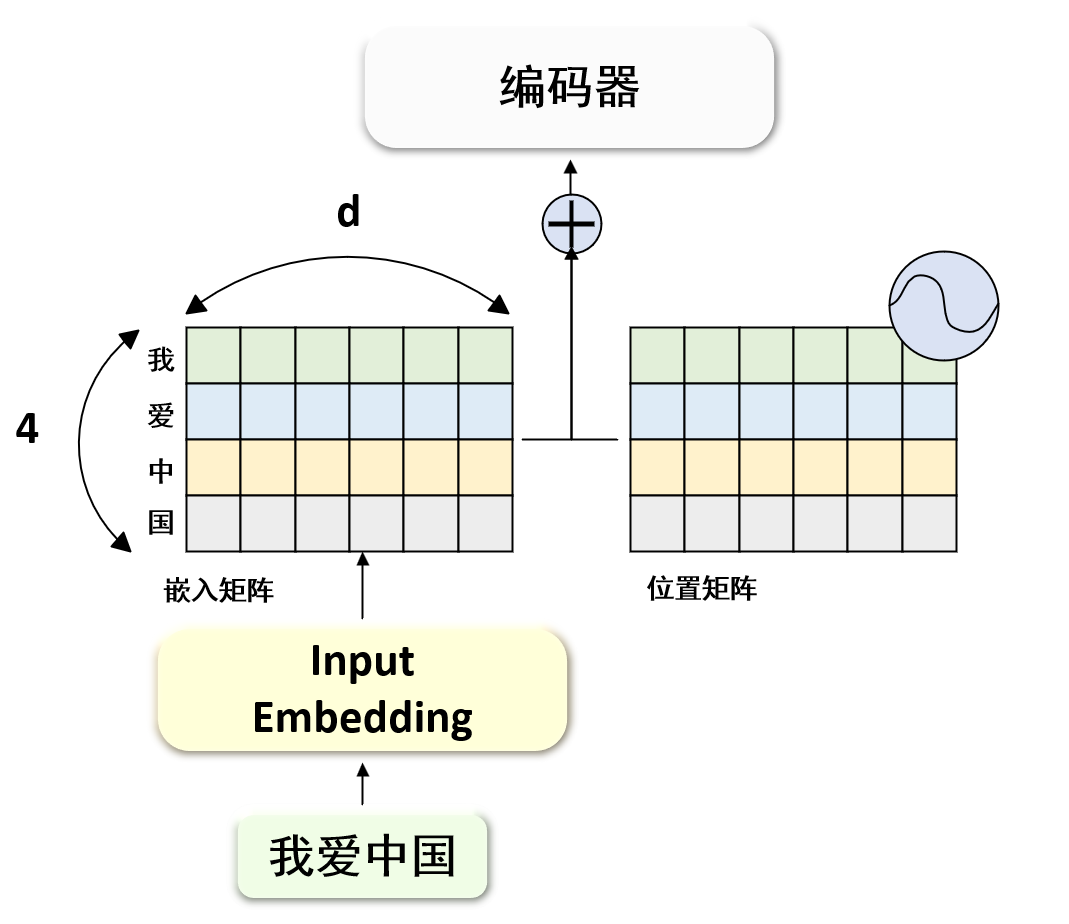
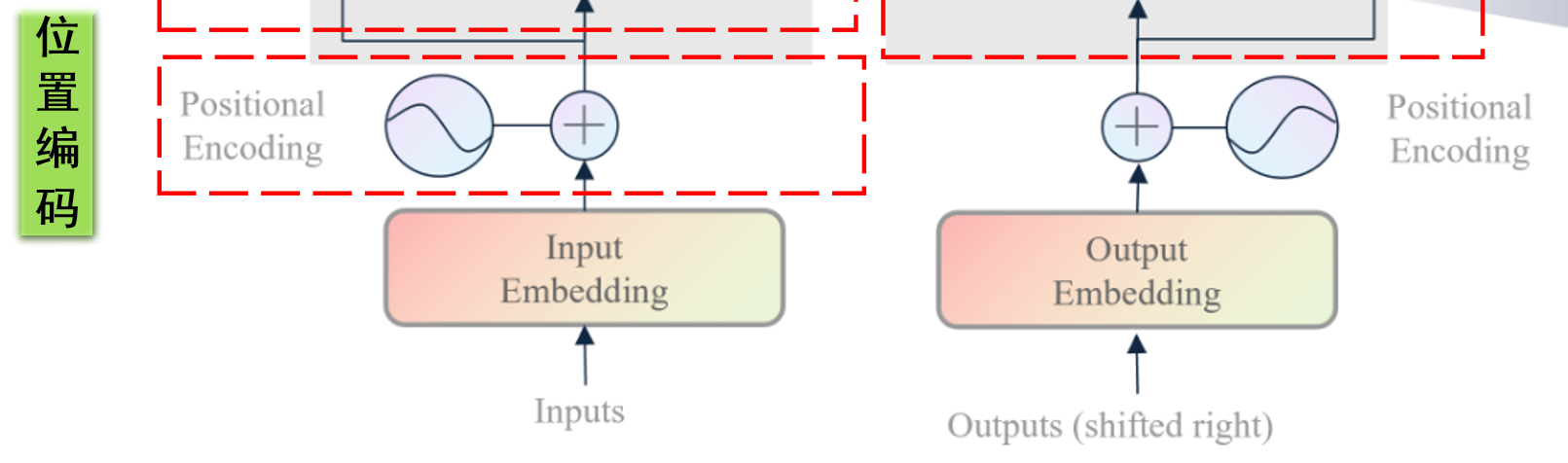
模型输入概述

无论是编码器的输入还是解码器的输入，他们接收的都是自然语言，因此需要设计一种把自然语言转化为向量的工具，这种工具就是词嵌入（input/output Embedding）。

此外，自然语言中一个句子中每个单词是具有时序顺序的，某个单词在不同位置表达的意思是完全不同，因此我们还需要一个标注每个单词位置的工具，这种工具就是位置编码（Positional Encoding）。

假设我们编码器输入端输入的中文句子是“我爱中国”，那么词嵌入（input/output Embedding）就会把这个由四个单词组成的句子转化成$4\times d$的矩阵，其中$d$是词嵌入的维度。此时位置编码（Positional Encoding）会把这个矩阵的每个元素加上位置编码信息，这样我们就得到了一个$4\times d$的矩阵，这个矩阵就是编码器的输入。

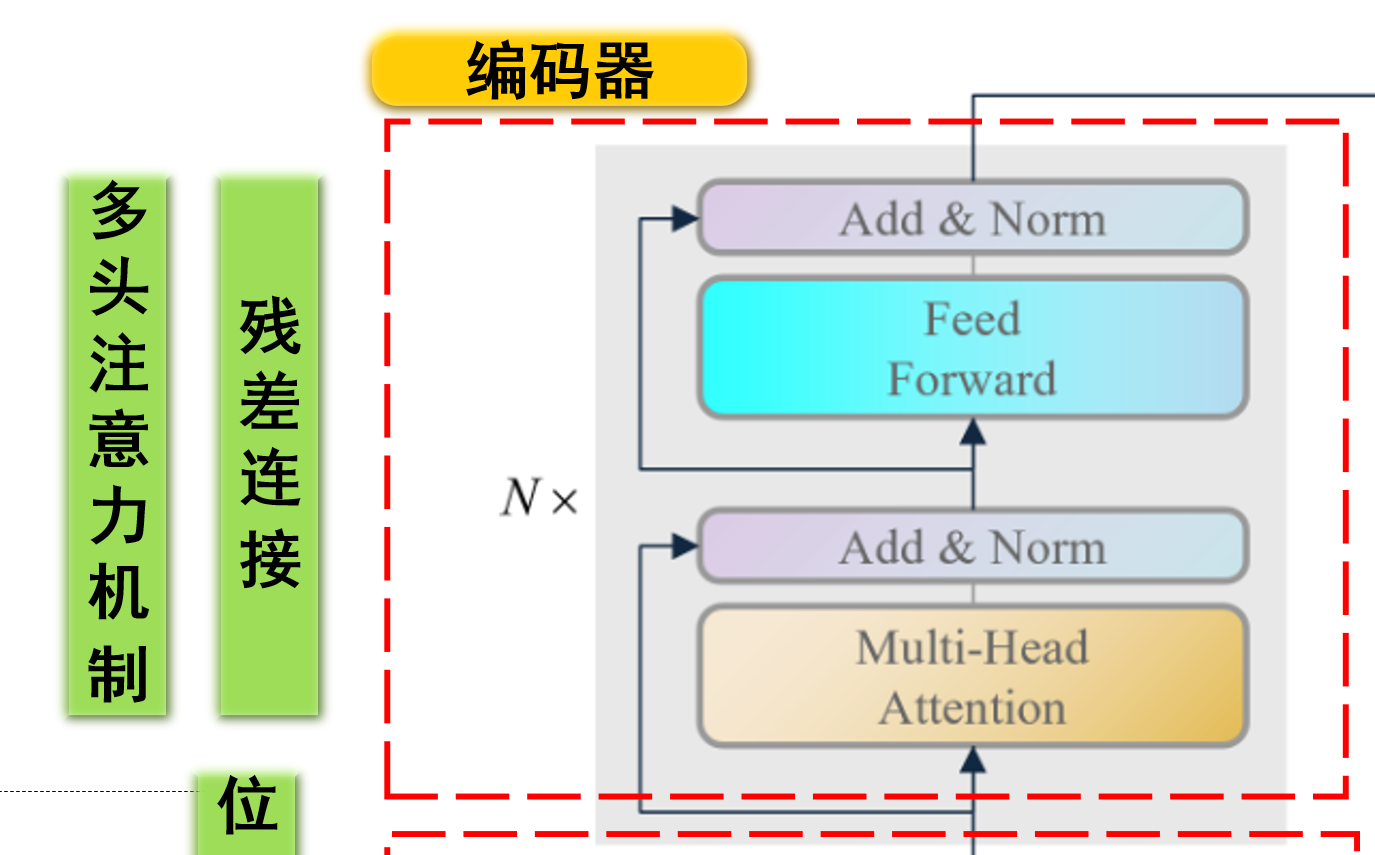
编码器概述

transformer编码器主要是针对原始序列的嵌入（经过位置编码后的）进行特征提取，它模仿人类的注意力机制和结合上下文的能力进行原始序列的理解。例如，我们有一个中文句子“我爱中国”，我们会注意到“我”和“爱”之间的关系是一个主谓关系，而“爱”和“中国”之间的关系是一个动宾关系，这种关系就是我们人类的注意力机制，transformer的编码器也会模仿这种关系，它擅长捕捉不同位置的不同单词之间的关系。

编码器有一个输入端，即原始序列嵌入输入，有一个输出端，即原始序列上下文特征。

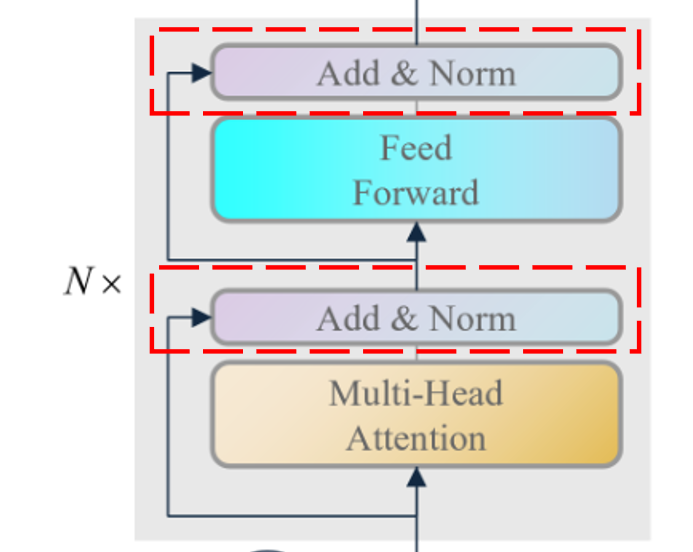
编码器主要由多头注意力机制（Muti-Head Attention）、前馈神经网络（Feed Forward）和若干残差块（Add & Norm）组成。此外一个transformer由多个编码器串联组成。下面是各个模块的作用：

• 多头注意力机制：多头注意力机制是为了让模型更好地提取到结合上下文的特征。
• 前馈神经网络：前馈神经网络是为了让模型提取深层特征。
• 残差块：残差块是为了让模型更好地提取到长期依赖的特征，防止梯度消失。

译码器概述

transformer译码器主要是针对原始序列的上下文特征和掩盖后目标序列的嵌入（经过位置编码后的）进行特征整合，最后预测完整的目标序列。例如，中文句子“我爱中国”经过特征提取后，输入到编码器端口一，英文翻译”I”嵌入输入到解码器端口二，那么transformer的译码器会结合“我爱中国”和“I”进行预测“love”、之后再根据“我爱中国”和“I love”预测“China”，这种设计可以让模型更好地提取到综合注意原文和译文的特征。

译码器有两个输入端，一个是原始序列上下文特征（编码器输出），一个是目标序列掩码嵌入输入，有一个输出端，即预测目标序列。

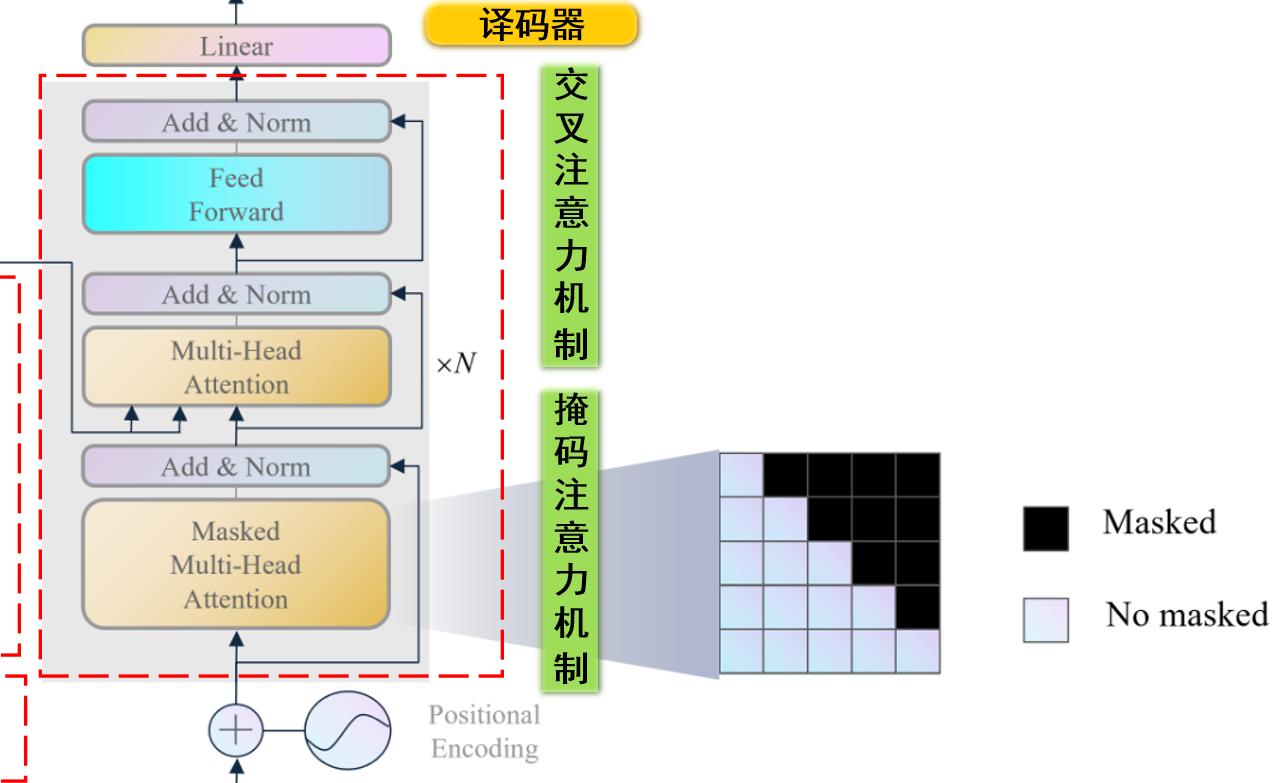
译码器主要由掩码多头注意力机制（Masked Muti-Head Attention）、多头注意力机制（Muti-Head Attention）、前馈神经网络（Feed Forward）和若干残差块（Add & Norm）组成。此外一个transformer由多个译码器串联组成。下面是各个模块的作用：

• 掩码多头注意力机制：掩码多头注意力机制是为了在提取目标序列上下文特征时，通过掩码防止模型看到未来的信息。
• 多头注意力机制：这里是交叉注意力机制，是为了让模型更好地提取到原始序列和目标序列的相互关系。
• 前馈神经网络：前馈神经网络是为了让模型提取深层特征。
• 残差块：残差块是为了让模型更好地提取到长期依赖的特征，防止梯度消失。

⭐位置编码模块

假设我们已经把自然语言转化获得了向量，即我们获得了嵌入矩阵$\boldsymbol X \in \mathbb{R}^{N \times d}$，其中$N$是句子长度，$d$是词嵌入的维度。

位置编码模块的作用是为了给每个词向量加上位置信息，便于模型学习到词向量的位置信息。因为transformer是一个无状态的模型，它不会像RNN一样记住上一个时间步的信息，所以我们需要设计一种机制让模型学习到词向量的位置信息。

• 模块输入：嵌入矩阵$\boldsymbol X \in \mathbb{R}^{N \times d}$，当输入某个句子的token（单词）数量不足$N$时，我们会用padding填充，并在计算注意力时不计算padding的位置。
• 模块输出: 编码后的矩阵$\boldsymbol X_{pos}\in \mathbb{R}^{N \times d}$。

位置编码计算

根据前文，位置编码是通过将原始嵌入矩阵$\boldsymbol X$与位置编码矩阵$\boldsymbol P$相加得到的，即$\boldsymbol X_{pos} = \boldsymbol X + \boldsymbol P$，下面我们来了解$\boldsymbol P$的计算方法。
transformer的位置编码是通过正弦和余弦函数交替计算得到的，即对于一个单词，第偶数维度使用正弦函数编码，第奇数维度使用余弦函数编码，其计算公式如下：

$$\begin{aligned} P_{pos, 2i} &= \sin(pos / 10000^{2i / d}) \\ P_{pos, 2i+1} &= \cos(pos / 10000^{2i / d}) \end{aligned}$$

其中，$pos$是单词的位置，$2i$和$2i+1$是维度，其计算示意图如下：

程序实现

class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len=5000, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.max_seq_len = max_seq_len
        self.dropout = nn.Dropout(p=dropout)

        # 初始化位置编码矩阵
        pe = torch.zeros(max_seq_len, d_model)

        # 计算位置编码
        for pos in range(max_seq_len):
            for i in range(d_model // 2):
                pe[pos, 2 * i] = math.sin(pos / 10000 ** ((2 * i) / d_model))
                pe[pos, 2 * i + 1] = math.cos(pos / 10000 ** ((2 * i) / d_model))

        # 增加 batch_size 维度
        pe = pe.unsqueeze(0)

        # 将pe加入模型，但是不进行更新
        self.register_buffer('pe', pe)

    def forward(self, x):
        seq_len = x.size(1)

        return self.dropout(x + self.pe[:, :seq_len, :])


# 测试代码
d_model = 512
pos_encoding = PositionalEncoder(d_model)
batch_size, seq_len = 64, 10
input_tensor = torch.rand(64, seq_len, d_model)
output_tensor = pos_encoding(input_tensor)
print(output_tensor.shape) # torch.Size([64, 10, 512])

程序中max_seq_len是我们设置的最大句子长度，即$N$，d_model是词嵌入的维度，即$d$。我们首先初始化位置编码矩阵pe即$\boldsymbol{P}$，然后计算位置编码，最后将pe加入模型，但是不进行更新。

注意程序中pe是一个buffer，它不会被更新，它被注册到缓冲区中，这样模型保存后，pe也会被保存到 state_dict() 中。方便直接调用。

⭐编码器模块

通过位置编码模块，我们已经得到了原始序列的位置编码后的嵌入矩阵$\boldsymbol X_{pos} \in \mathbb{R}^{N \times d}$，接下来我们需要对这个矩阵进行结合上下文的特征提取，这就是编码器模块的作用。

编码器模块主要由多头注意力机制、前馈神经网络和若干残差块组成，下面我们来了解各个模块的作用。

✨多头注意力机制

• 模块输入：原始序列位置编码后的嵌入矩阵$\boldsymbol X_{pos} \in \mathbb{R}^{N \times d}$。
• 模块输出：原始序列上下文特征$\boldsymbol X_{multi-att} \in \mathbb{R}^{N \times d}$。

多头注意力机制是为了让模型更好地提取到结合上下文的特征，它主要由查询（Q）、键（K）、值（V）和注意力分数（Attention Score）组成，下面我们来了解多头注意力机制的计算过程。首先从自注意力机制说起。

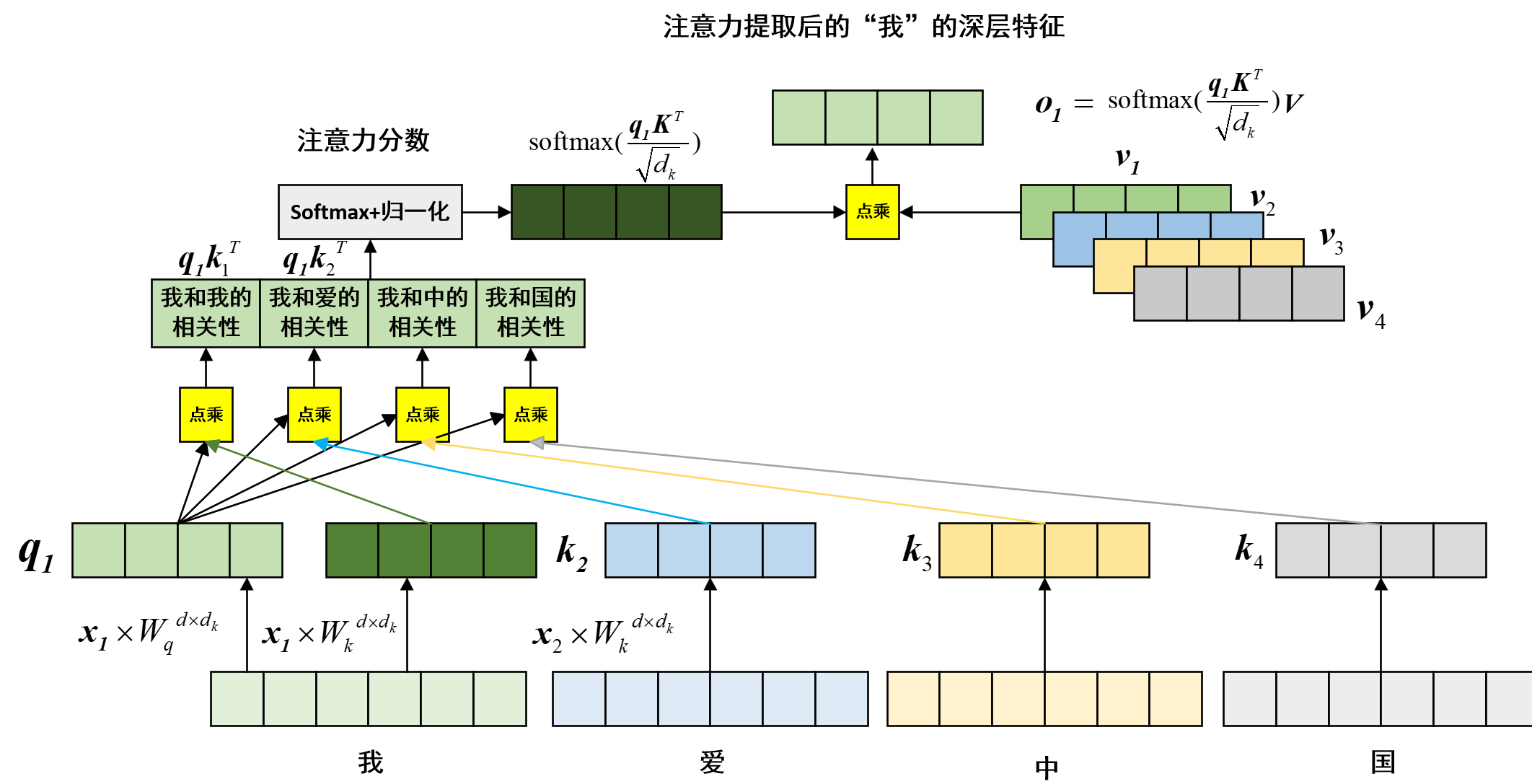
☀️自注意力机制

现在对于中文句子“我爱中国”，我们先举一个自注意力的简单例子：只计算“我”和其他词的注意力关系，我如何计算“我”这个词的注意力分数：我怎么衡量“我”和“爱”、“中”、“国”之间的关系？，见下图：

我们回忆，在线性代数中，俩个向量相似是不是可以用点积来衡量？我们可以用点积来衡量“我”和“爱”、“中”、“国”之间的关系，但是实际上，“我”这个词和“爱”的差别很大，他们内积是根本体现不出来相似性的。这是不是就不能用点积来衡量了呢？

答案是可以的，实际上，表面上“我”和“爱”、“中”、“国”之间差别很大，但是映射到其他特征空间呢？他们必定具有潜在的相似性，我们在潜在的特征空间再计算点积，就可以衡量他们之间的相似性了。

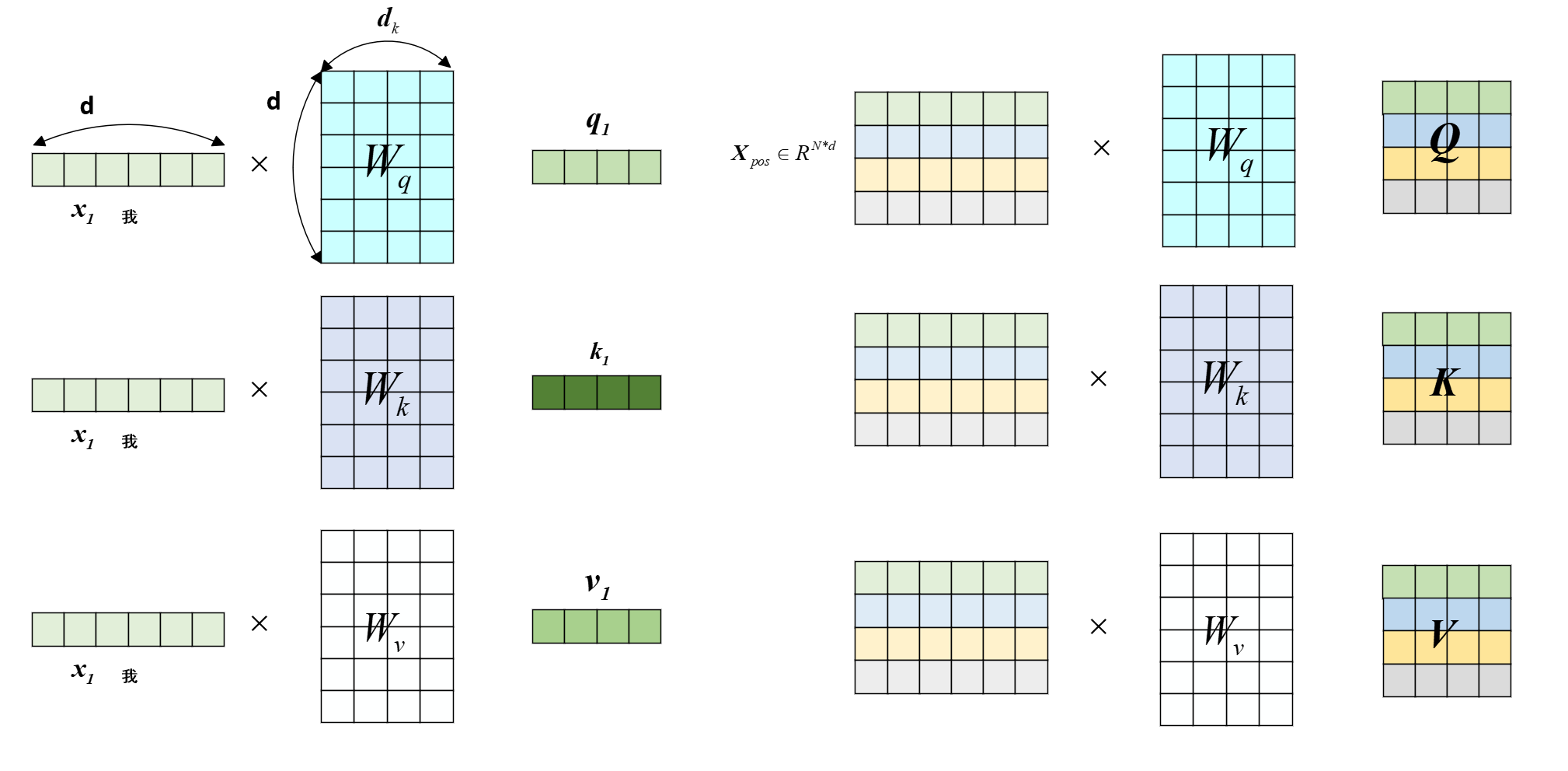
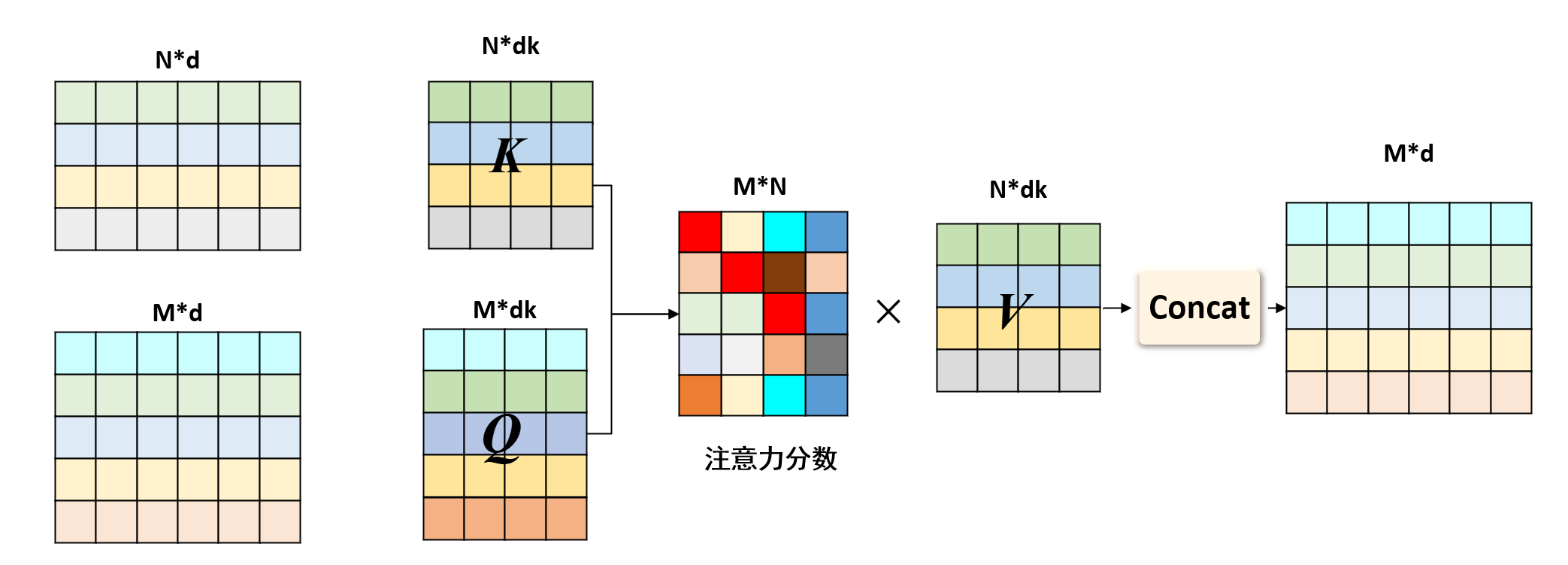
假设“我”经过位置编码后的词嵌入向量是$\boldsymbol x_1 \in \mathbb{R}^{1 \times d}$(即$\boldsymbol x_1 = \boldsymbol X_{pos}[1]$)，“爱”、“中”、“国”分别是$\boldsymbol x_2$、$\boldsymbol x_3$、$\boldsymbol x_4$。自注意力机制首先将每个单词分别映射到查询空间（Q，Query）、键空间（K，Key）和值空间（V，Value）。具体是通过权值矩阵$\boldsymbol W^Q \in \mathbb{R}^{d \times d_k}$、$\boldsymbol W^K \in \mathbb{R}^{d \times d_k}$、$\boldsymbol W^V \in \mathbb{R}^{d \times d_k}$分别映射到查询空间、键空间和值空间，即以$\boldsymbol x_1$为例：

$$\begin{aligned} \boldsymbol q_1 &= \boldsymbol x_1 \boldsymbol W^Q \\ \boldsymbol k_1 &= \boldsymbol x_1 \boldsymbol W^K \\ \boldsymbol v_1 &= \boldsymbol x_1 \boldsymbol W^V \\ \end{aligned}$$

其中，$\boldsymbol q_1 \in \mathbb{R}^{1 \times d_k}$、$\boldsymbol k_1 \in \mathbb{R}^{1 \times d_k}$、$\boldsymbol v_1 \in \mathbb{R}^{1 \times d_k}$，$d_k$是查询空间、键空间和值空间的维度。

$\boldsymbol q_1$用于查询和其他单词的相似度，它乘以其他单词的键$\boldsymbol k_1$、$\boldsymbol k_2$、$\boldsymbol k_3$、$\boldsymbol k_4$，得到注意力分数，即：

$$\begin{aligned} \boldsymbol s_{1,1} &= \boldsymbol q_1 \boldsymbol k_1^T \\ \boldsymbol s_{1,2} &= \boldsymbol q_1 \boldsymbol k_2^T \\ \boldsymbol s_{1,3} &= \boldsymbol q_1 \boldsymbol k_3^T \\ \boldsymbol s_{1,4} &= \boldsymbol q_1 \boldsymbol k_4^T \\ \end{aligned}$$

设$\boldsymbol{K} = \begin{bmatrix}
\boldsymbol{k}_1 \\
\boldsymbol{k}_2 \\
\boldsymbol{k}_3 \\
\boldsymbol{k}_4
\end{bmatrix} \in \mathbb{R}^{4 \times d_k}$，则可以把上式写成矩阵形式：

$$\boldsymbol s_1 = \boldsymbol q_1 \boldsymbol K^T$$

其中$\boldsymbol s_1$ 表示”我”关于所有单词的注意力分数。然而这里得到的注意力分数需要进行归一化和softmax(使得所有元素的注意力分数总和为1)，即：

$$\boldsymbol a_1 = \text{softmax}(\frac{\boldsymbol s_1}{\sqrt{d_k}})$$

之后，我们直接将注意力分数$\boldsymbol a_1$作为权值乘以对应值向量$\boldsymbol v_1$、$\boldsymbol v_2$、$\boldsymbol v_3$、$\boldsymbol v_4$，得到最终的“我”的注意力输出：

$$\boldsymbol o_1 = \boldsymbol a_{1,1} \boldsymbol v_1 + \boldsymbol a_{1,2} \boldsymbol v_2 + \boldsymbol a_{1,3} \boldsymbol v_3 + \boldsymbol a_{1,4} \boldsymbol v_4$$

其中，$\boldsymbol o_1$是“我”的注意力输出、$\boldsymbol a_{1,1}$、$\boldsymbol a_{1,2}$、$\boldsymbol a_{1,3}$、$\boldsymbol a_{1,4}$是“我”和“爱”、“中”、“国”之间的注意力分数。设$\boldsymbol V = \begin{bmatrix}
\boldsymbol v_1 \\
\boldsymbol v_2 \\
\boldsymbol v_3 \\
\boldsymbol v_4 \end{bmatrix} \in \mathbb{R}^{4 \times d_k}$，则可以把上式写成矩阵形式：

$$\boldsymbol o_1 = \boldsymbol a_1 \boldsymbol V = \text{softmax}(\frac{\boldsymbol q_1 \boldsymbol K^T}{\sqrt{d_k}}) \boldsymbol V$$

以上只是计算“我”这个词的注意力输出，对于其他词也是一样的计算过程，最后我们将所有词的注意力输出拼接起来，得到原始序列的上下文特征$\boldsymbol X_{single-att}$。读者可以自己整理对于输入矩阵$\boldsymbol X_{pos}$的计算过程。

假设输入矩阵$\boldsymbol X_{pos}$获得Q矩阵$\boldsymbol Q$、K矩阵$\boldsymbol K$、V矩阵$\boldsymbol V$，则自注意力机制的计算过程如下：

$$\color{red} \boldsymbol X_{single-att} = \text{softmax}(\frac{\boldsymbol Q \boldsymbol K^T}{\sqrt{d_k}}) \boldsymbol V$$

此时，自注意力提取的上下文特征$\boldsymbol X_{single-att}\in \color{red} \mathbb{R}^{N \times d_k}$，显然，如果想让自注意力前后形状不变，就设定QKV空间维度$d_k=d$，这样的话，我们就使用了3个可学习的权值矩阵$\boldsymbol W^Q$、$\boldsymbol W^K$、$\boldsymbol W^V$，这样我们就得到了原始序列的自注意力机制提取的上下文特征，且保证形状不变。

然而，3个可学习的权值矩阵会不会不够用呢？我们能不能用更多的权值矩阵来提取更多层次、更潜在、更复杂的特征呢，答案是可以的，这就是多头注意力机制的设计。

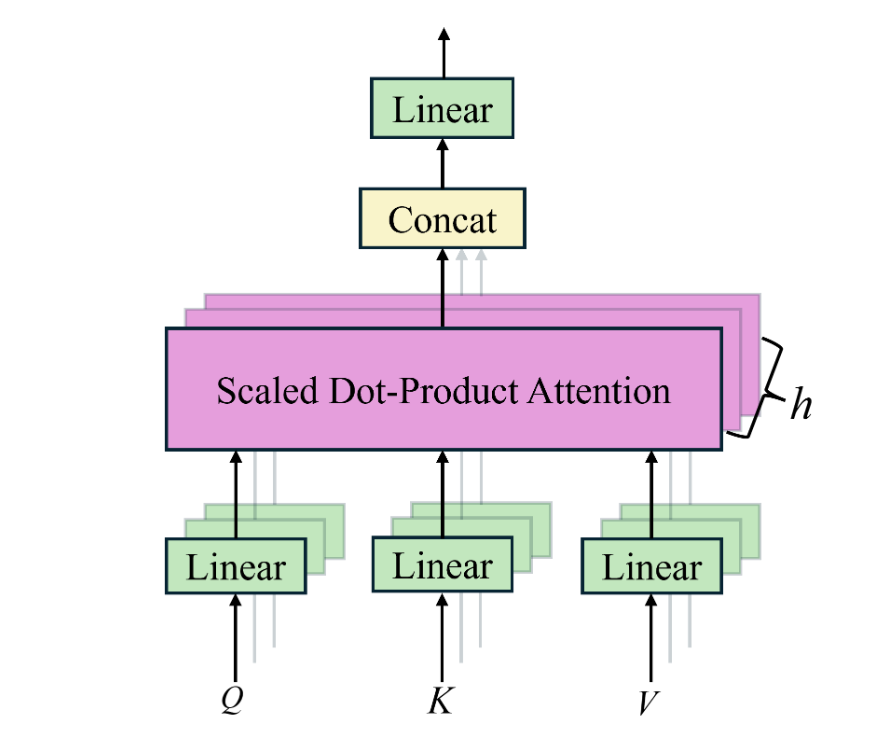
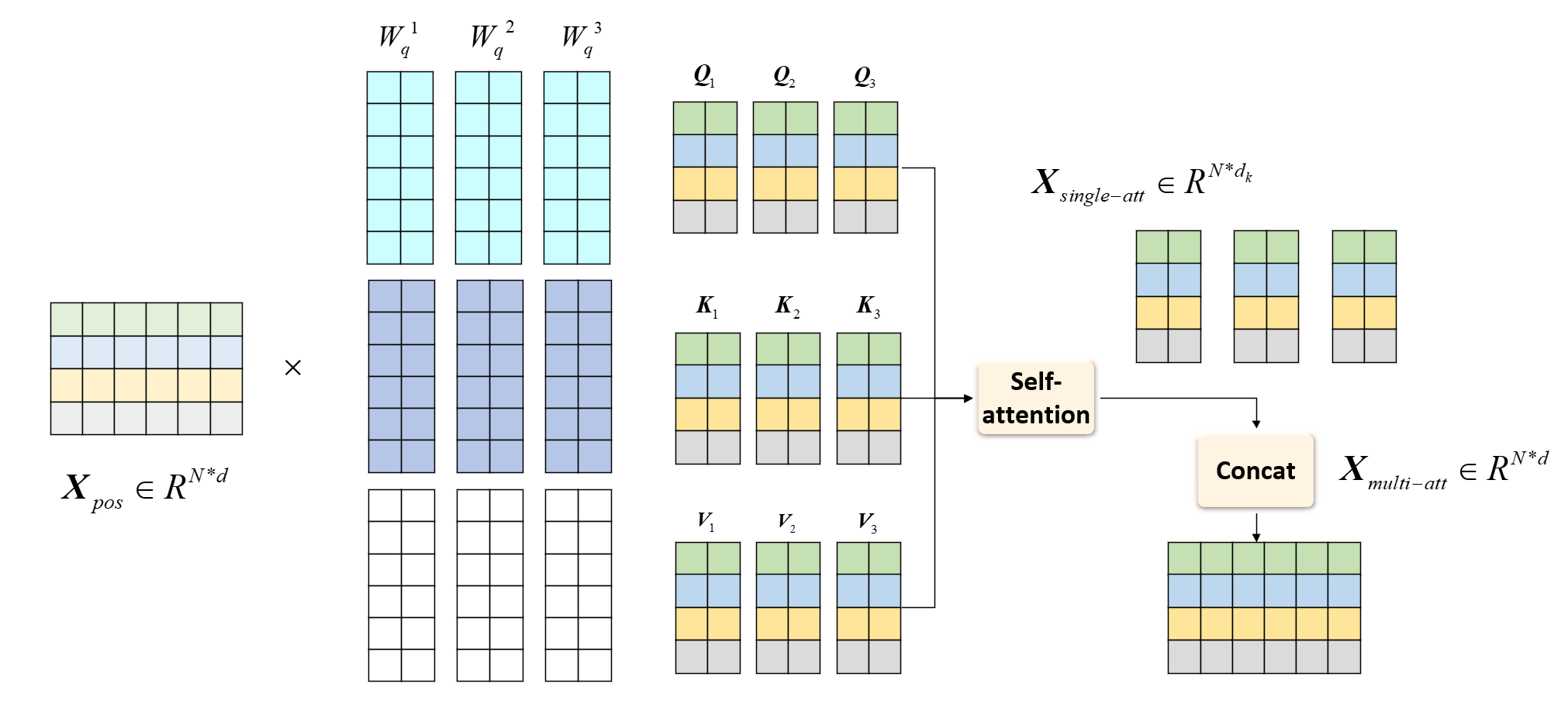
☀️多头注意力机制

多头注意力机制相对于自注意力机制，就是多个自注意力机制的拼接，设想一下，对于自注意力机制，如果我们QKV空间维度$d_k \neq d$，那我们提取出的特征形状就会和原始序列的形状不一样，即有：

$$\boldsymbol X_{single-att} \in \mathbb{R}^{N \times d_k} \neq \boldsymbol X_{pos} \in \mathbb{R}^{N \times d}$$

如果这样设计呢：我们使用$h$个自注意力机制拼接起来，每个自注意力机制的QKV空间维度$d_k=d/h$，这样我们就可以使用$h$个自注意力输出拼接（Concat）起来，得到原始序列的上下文特征$\boldsymbol X_{multi-att}$，且保证形状不变，即：

$$\boldsymbol X_{multi-att} \in \mathbb{R}^{N \times d} = \text{Concat}(\boldsymbol X_{single-att}^1, \boldsymbol X_{single-att}^2, \cdots, \boldsymbol X_{single-att}^h)$$

其中，$\boldsymbol X_{single-att}^i \in \mathbb{R}^{N \times d_k}$是第$i$个自注意力机制提取的上下文特征，共有$h$个自注意力机制。这样我们就有了$3h$个可学习的Q,K和V权值矩阵，这就是多头注意力机制的设计，下图是多头注意力机制的计算过程：

示意图中就假设了输入维度$d=6$，多头注意力机制的头数$h=3$，QKV空间维度$d_k=2$，这样我们就有了$3h=9$个可学习的权值矩阵，这样我们就可以提取到更多层次、更潜在、更复杂的特征。注意编码器的多头注意力机制中的Q、K、V均是由原始序列位置编码后的嵌入矩阵$\boldsymbol X_{pos}$得到的（解码器会有所不同）

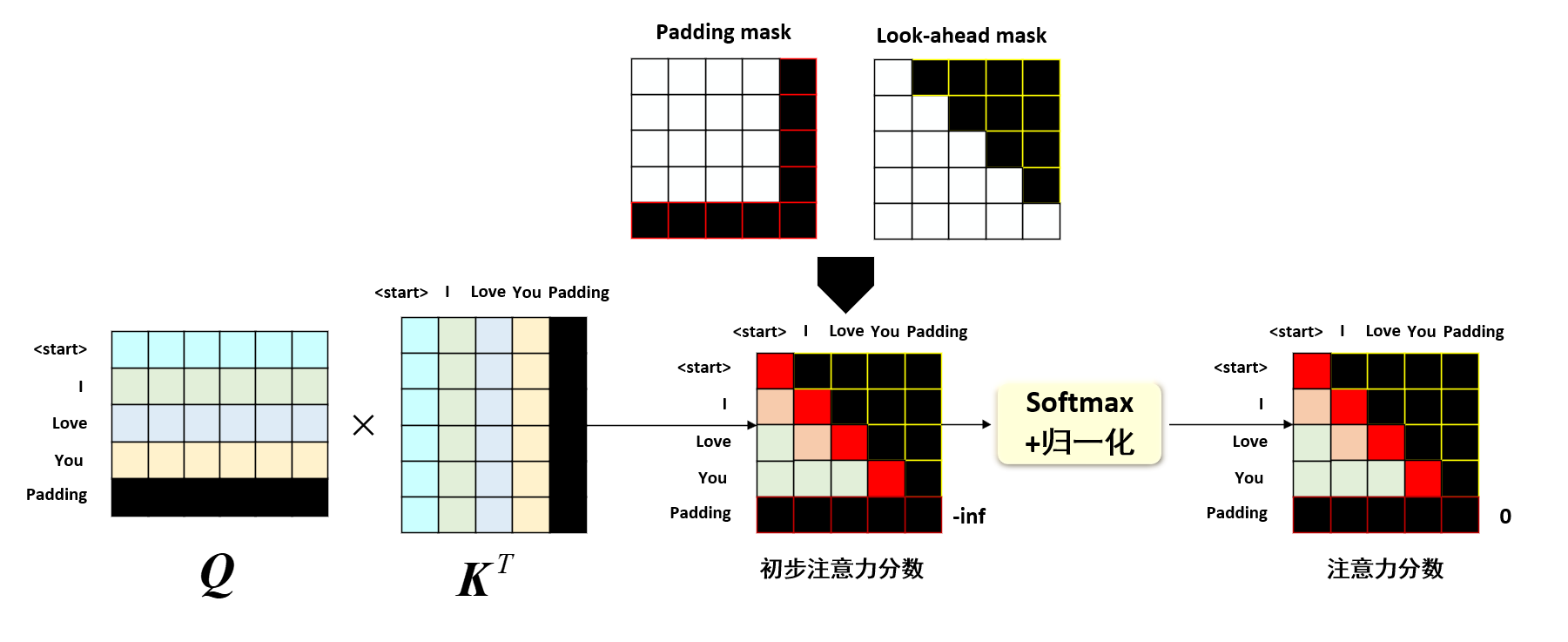
注意如前文所说，由于训练数据句子长度不一样，即对于短句子我们会用padding填充，所以我们会在计算注意力时不计算padding的位置，这就是transfomer的**Padding mask机制，这里我们暂时不做介绍，后续将统一在解码器中的掩码多头注意力机制中介绍。

transformer中多头注意力机制中有俩种mask机制，一种是Padding mask机制，另一种是Look-ahead mask机制，这是一种防止模型提前看到目标序列的机制，这种机制只会出现在解码器多头注意力机制中。

多头自注意力模块 程序实现

class MultiheadAttention(nn.Module):
    def __init__(self, d_model, num_heads=8, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_k = d_model // num_heads

        # W_Q, W_K, W_V
        self.q_linear = nn.Linear(d_model, d_model)
        self.k_linear = nn.Linear(d_model, d_model)
        self.v_linear = nn.Linear(d_model, d_model)

        self.dropout = nn.Dropout(p=dropout)

        # W_O
        self.out_linear = nn.Linear(d_model, d_model)

    def forward(self, query, key, value, mask=None):
        batch_size = key.size(0)

        # 对输入进行线性变换得到Q, K, V, 然后按头数拆分，最后调整成形状[batch_size, num_heads, seq_len, d_k]
        # 目的就是为了后续计算过程中，各个head之间的独立计算，具体可参考上面详细例子示意
        q = self.q_linear(query).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        k = self.k_linear(key).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        v = self.v_linear(value).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

        scores = torch.matmul(q, k.transpose(-2, -1) / math.sqrt(self.d_k))

        if mask is not None:  # mask 是为了在decode过程中用
            mask = mask.unsqueeze(1)  # 增加一个head维度
            scores = scores.masked_fill(mask == 0, float('-inf'))

        scores = F.softmax(scores, dim=-1)  # -1代表最后一个维度，这里就是为了表示对每一行的元素进行操作

        # 这里实现的就是多个head输出后，然后concatenation
        attention_output = torch.matmul(scores, v).transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)

        # 线性变换得到最后输出
        output = self.out_linear(attention_output)

        return output


# 测试代码
inputs = torch.tensor([
    [[1, 2, 3, 4, 5, 6],
     [2, 3, 4, 5, 6, 7],
     [3, 4, 5, 6, 7, 8],
     [3, 4, 5, 6, 7, 8],
     [3, 4, 5, 6, 7, 8],
     [4, 5, 6, 7, 8, 9]]
], dtype=torch.float32)

num_heads = 2
d_model = 6

multihead_self_attention = MultiheadAttention(d_model, num_heads)
output = multihead_self_attention(query=inputs, key=inputs, value=inputs)

print(output.shape)  # torch.Size([1, 6, 6])

程序中的d_model是词嵌入的维度，num_heads是多头注意力机制的头数，mask即是输入的padding mask选项。我们首先将输入query、key、value通过线性变换得到Q、K、V，然后按头数拆分，最后调整成形状[batch_size, num_heads, seq_len, d_k]，目的就是为了后续计算过程中，各个head之间的独立计算，具体可参考上面详细例子示意。

✨残差&归一化模块

残差和归一化模块是为了让模型在深层网络中更加稳定，通过残差连接，模型会避免忘记之前的特征，通过归一化，模型训练会更加稳定，transformer中有多次残差和归一化模块，即图中的Add & Norm。残差块和归一化模块不会改变模型的输入输出形状，只是对输入进行加和和归一化。

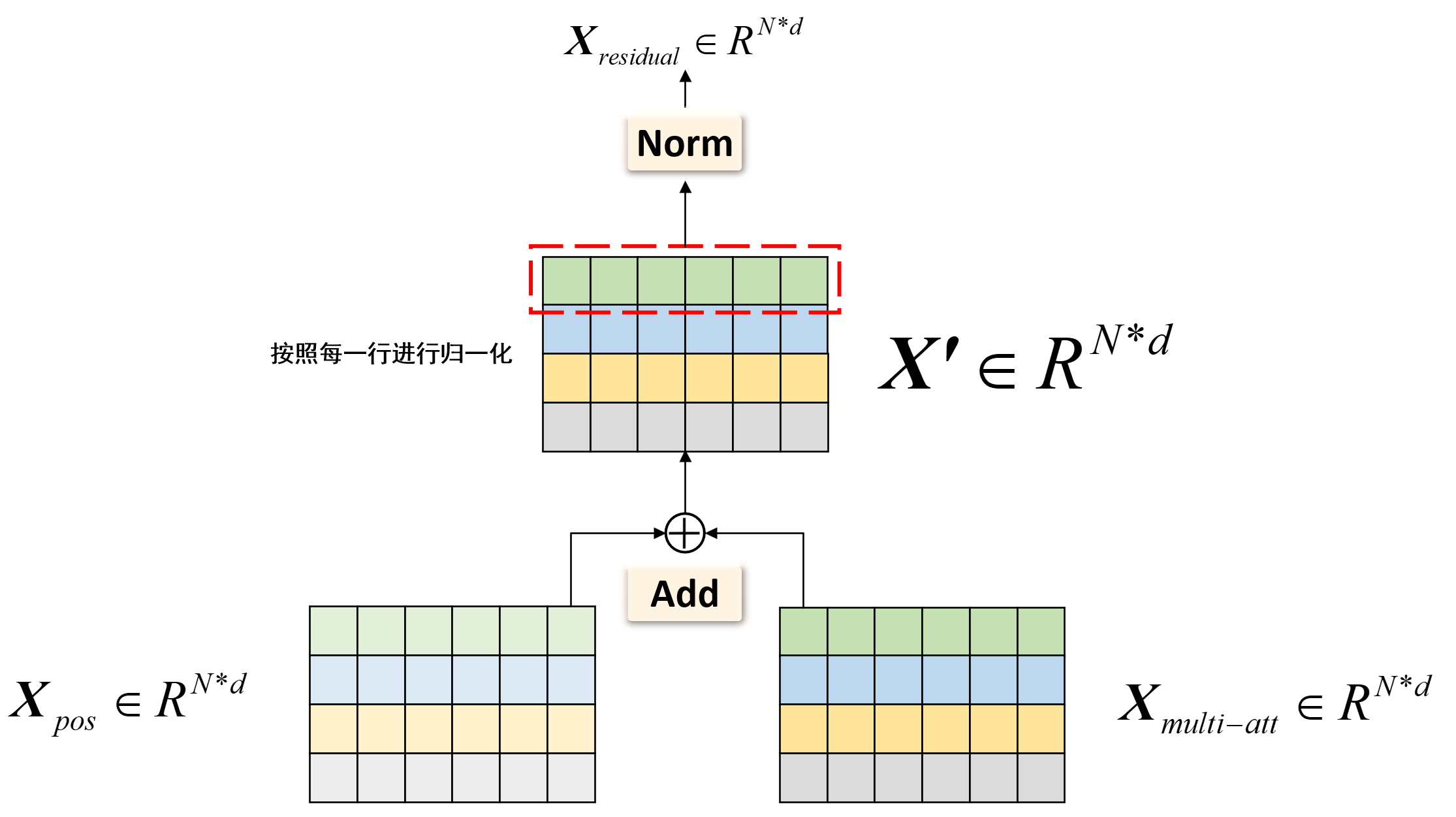
• 模块输入：俩个输入$\boldsymbol X_{multi-att} \in \mathbb{R}^{N \times d}$和$\boldsymbol X_{pos} \in \mathbb{R}^{N \times d}$。(这里只以第一次出现的残差块为例，其他地方读者同理)
• 模块输出：残差块的输出$\boldsymbol X_{residual} \in \mathbb{R}^{N \times d}$。

transformer中残差块总连接在注意力机制的前后 或 前馈网络的前后！

残差块的设计十分简单，就是将输入和输出进行加和，即Add，之后对加和后的结果进行归一化，即Norm，这样就得到了残差块的输出。记住，transformer中的残差块使用的是层归一化（Layer Normalization），即对每个样本的每个特征进行归一化，而不是对每个样本进行归一化。

在机器学习中，层归一化的计算公式如下，对于输入的$\boldsymbol X’ \in \mathbb{R}^{N \times d}$，我们有：

$$x_{residual}^{i,j} = \frac{x'_{i,j} - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}} \cdot \gamma_j + \beta_j$$

其中，$\mu_i$是第$i$行特征的均值，$\sigma_i^2$是第$i$行特征的方差，$\gamma_j$和$\beta_j$是可学习的参数，它们属于第$j$特征列，$\epsilon$是一个很小的数，防止分母为0。这意味计算全部归一化，总共有$N$个均值和方差，$d$个$\gamma_j$和$\beta_j$。
Qustion：为什么要使用层归一化而不是批归一化呢？
Answer：因为批归一化是对每个特征的每个样本进行归一化，而transformer中的残差块是对每个样本的所有特征进行归一化，简单的说，对于“我爱中国”这个句子，经过位置编码和注意力机制后，我们得到的$\boldsymbol X_{multi-att} \in \mathbb{R}^{N \times d}$。层归一化就是对每个样本的所有特征进行归一化，即先对“我”这个$1 \times d$的向量进行归一化，再对“爱”这个$1 \times d$的向量进行归一化，以此类推。而批归一化是对每个特征的所有样本进行归一化，即先对“我”，“爱”，“中”，“国”这4个$1 \times d$的向量取第一个元素，即对$4 \times 1$的向量进行归一化。
综上所述，Batch Normalization是对每个特征所有样本进行归一化，即对列进行归一化，因为这些特征在统计上是相关的，所以它们可以被合理地放在一起进行归一化处理。这就像是在同一个班级里，比较不同学生的同一科目成绩，因为这些成绩都在相同的评分标准下，所以可以直接比较。
相反，Layer Normalization是对每个样本的所有特征进行归一化，即对行进行归一化，因为这些特征在统计上是不相关的，所以它们不能被合理地放在一起进行归一化处理。LayerNorm的解决方案是对每个样本的所有特征进行单独归一化，而不是基于整个批次。这就像是评估每个学生在所有科目中的表现，而不是仅仅关注单一科目，这样可以更全面地理解每个学生的整体表现。
显然，所有单词的嵌入的某一维度的特征之间的毫无相关的，所以使用Layer Normalization。

残差块 程序实现

class LayerNorm(nn.Module):
    def __init__(self, d_model, eps=1e-6):
        super().__init__()

        self.gamma = nn.Parameter(torch.ones(d_model))
        self.beta = nn.Parameter(torch.zeros(d_model))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)  # -1代表最后一个维度，对每一行元素进行操作
        var = x.var(-1, keepdim=True) # -1代表最后一个维度，对每一行元素进行操作

        return self.gamma * (x - mean) / torch.sqrt(var + self.eps) + self.beta


# 测试代码
input_tensor = torch.tensor([[1.0, 2.0, 3.0],
                             [4.0, 5.0, 6.0]])
layer_norm = LayerNorm(d_model=3)
normed_reuslt = layer_norm(input_tensor)
print(normed_reuslt)
# tensor([[-1.0000,  0.0000,  1.0000],
#         [-1.0000,  0.0000,  1.0000]], grad_fn=<AddBackward0>)

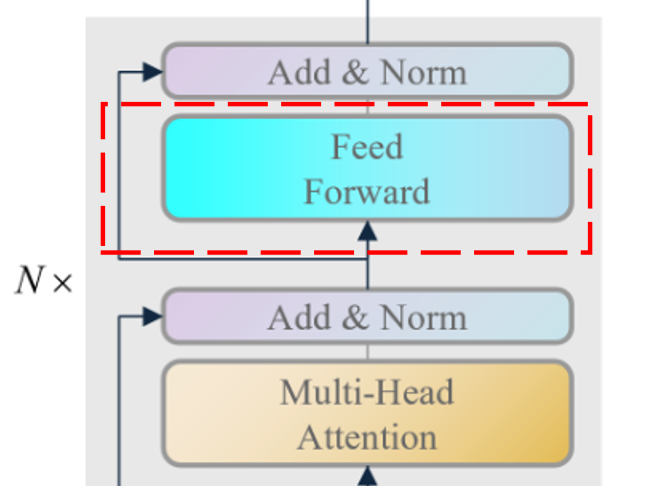
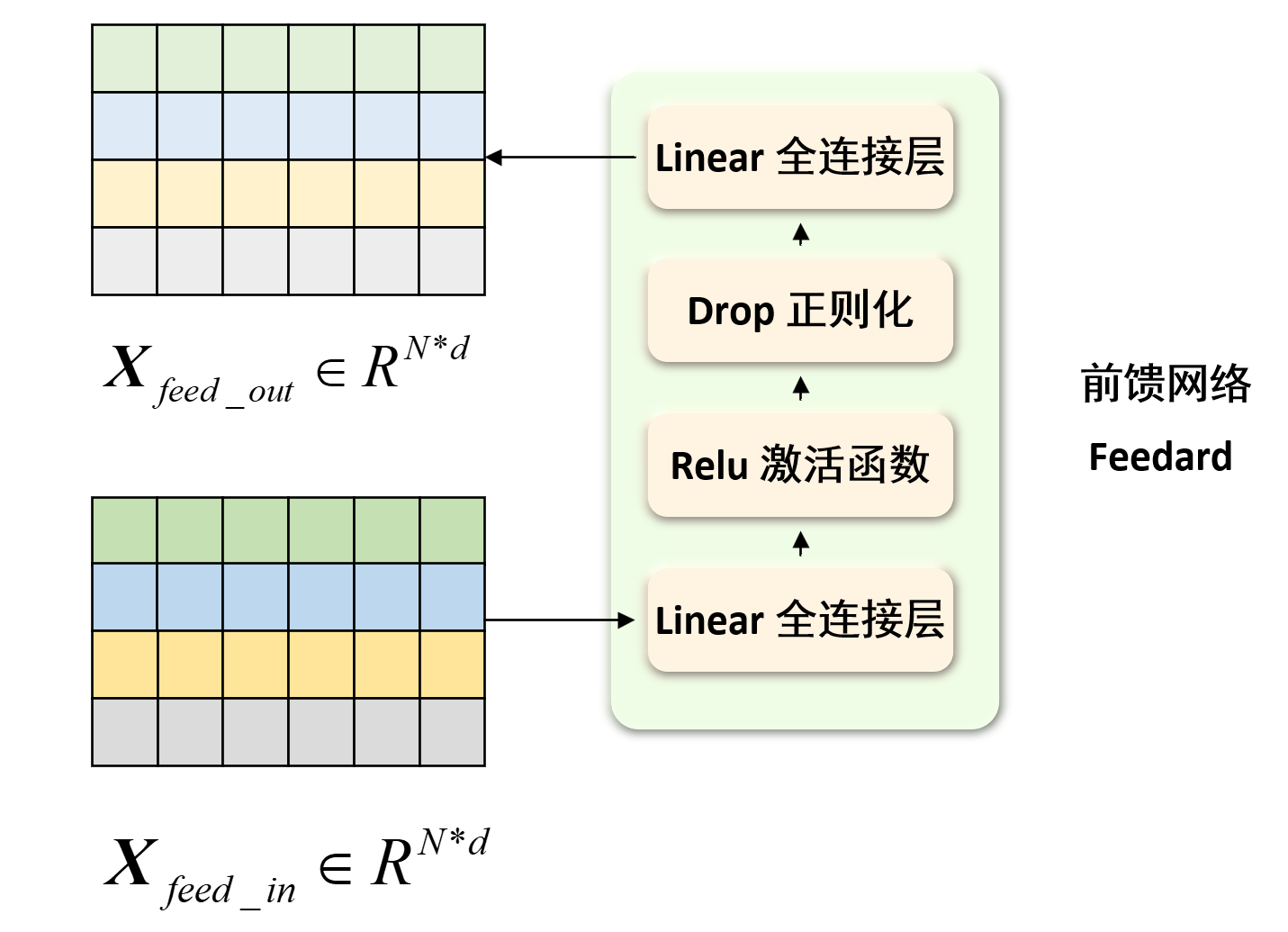
✨前馈神经网络模块

• 模块输入：残差块的输出$\boldsymbol X_{feed_in} \in \mathbb{R}^{N \times d}$。
• 模块输出：前馈神经网络的输出$\boldsymbol X_{feed_out} \in \mathbb{R}^{N \times d}$。

前馈神经网络模块是为了让模型能够提取到更高层次、更复杂的特征，它主要由两层全连接层、正则化和激活函数ReLU组成，下面我们来了解前馈神经网络模块的计算过程。

其中全连接层就是为了提取更高层次、更复杂的特征，正则化是为了让模型训练更加稳定，激活函数ReLU是为了引入非线性，使得模型能够拟合更复杂的函数，最后一个全连接层就是为了把输出的相形状的特征映射到原始特征空间，这样就得到了前馈神经网络模块的输出。因此可能第一个全连接层的输出维度是$d \rightarrow d_{ff}$，第二个全连接层的输出维度是$d_{ff} \rightarrow d$。

前馈神经网络模块 程序实现

class FeedForward(nn.Module):
    def __init__(self, d_model, hidden_size=2048, dropout=0.1):
        super().__init__()

        self.linear1 = nn.Linear(d_model, hidden_size)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(p=dropout)
        self.linear2 = nn.Linear(hidden_size, d_model)

    def forward(self, x):
        x = self.linear1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.linear2(x)

        return x


# 测试代码
d_model = 512
x = torch.randn(64, 10, 512)
ff_layer = FeedForward(d_model)
output = ff_layer(x)
print(output.shape)  # torch.Size([64, 10, 512])

程序中，hidden_size是前馈神经网络的隐藏层维度，即$d_{ff}$，我们首先将输入x通过第一个全连接层得到linear1，然后通过激活函数ReLU，再通过dropout正则化，最后通过第二个全连接层得到输出。这样就得到了前馈神经网络模块的输出。

完整编码层 程序实现

class EncodeLayer(nn.Module):
    def __init__(self, d_model, num_heads=8, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads

        self.layer_norm = LayerNorm(d_model)
        self.multi_attention = MultiheadAttention(d_model, num_heads)
        self.ff_layer = FeedForward(d_model)

        self.dropout = nn.Dropout(p=dropout)

    def forward(self, x):
        _x = x  # 先存储输入，用于后面和attention输出进行残差连接
        x = self.layer_norm(x)  # 输入到attention之前新进行层归一化
        x = self.dropout(self.multi_attention(query=x, key=x, value=x))  # attention 输出
        __x = x  # 存储attention的输出， 用于后面和feedforward的输出残差连接
        x = self.layer_norm(_x + x)  # 对 add之后的结果 norm
        x = self.dropout(self.ff_layer(x))  # feedforward 输出
        x = __x + x  # 残差连接

        return x
        
# 测试代码
# d_model = 512
# x = torch.randn(64, 10, 512)
# encode_layer = EncodeLayer(d_model)
# output = encode_layer(x)
# print(output.shape)  # torch.Size([64, 10, 512])       

完整编码器模块 程序实现

class Encode(nn.Module):
    def __init__(self, d_model, vocab_size=2000,  num_encode_layer=6, num_heads=8, dropout=0.1):
        super().__init__()

        self.vocab_size = vocab_size
        self.d_model = d_model
        self.num_encode_layer = num_encode_layer
        self.num_heads = num_heads
        self.dropout = dropout

        self.embed = nn.Embedding(vocab_size, d_model)  # 定义词典大小

        self.position_encode = PositionalEncoder(d_model)
        self.encode_layer = EncodeLayer(d_model)

        # 六个EncodeLayer层
        self.encode_layers = nn.ModuleList([copy.deepcopy(self.encode_layer) for i in range(num_encode_layer)])

        self.layer_norm = LayerNorm(d_model)

    def forward(self, src):
        x = self.embed(src)
        x = self.position_encode(x)

        # 六个EncodeLayer层依次输出
        for i in range(self.num_encode_layer):
            x = self.encode_layers[i](x)

        return self.layer_norm(x)


# 测试代码
d_model = 512
x = torch.LongTensor([[1, 2, 4]])  # 输入是形状为： [batch_size, seq_length]， 这里batch_zie = 1, seq_len = 3
encode = Encode(d_model=d_model)
output = encode(x)
print(output.shape)  # torch.Size([1, 3, 512])

程序中，vocab_size是词典大小，d_model是词嵌入的维度，num_encode_layer是编码器的层数，num_heads是多头注意力机制的头数，我们首先将输入src通过词嵌入层得到embed，然后通过位置编码层得到position_encode，之后通过num_encode_layer个编码器层得到输出，最后通过层归一化得到最终的输出。（词嵌入的过程不在这里赘述）

⭐译码器模块

通过编码器模块，我们已经得到了原始序列的上下文特征$\boldsymbol X_{en} \in \mathbb{R}^{N \times d}$，接下来我们结合原始序列的上下文特征去预测目标序列，在训练时，目标序列会直接给出，但是为了避免在预测时提前看到答案，transformer设计了掩码多头注意力机制进行目标序列的掩盖，之后让模型使用交叉注意力机制结合原始序列的上下文特征和掩盖后的目标序列上下文特征进行预测下一个单词，下面我们来了解译码器模块的各个模块。

注意译码器中也包含有前馈神经网络和残差块，但是在transformer中，译码器的前馈神经网络和残差块的设计和编码器是一样的，所以这里不再赘述，下面我们主要来了解译码器模块的掩码多头注意力机制和交叉注意力机制。

✨掩码多头注意力机制

前面在介绍编码器的多头自注意力机制时，我们已经介绍了transformer中的多头注意力机制有俩种掩码设计，一种是Padding mask机制，这种主要是解决编码输入句子长度不一样的问题，另一种是Look-ahead mask机制，这种主要是解决解码器提前看到目标序列的问题。

• 模块输入：目标序列的位置编码后嵌入矩阵$\boldsymbol Y_{pos} \in \mathbb{R}^{M \times d}$。
• 模块输出：掩码多头注意力机制的输出$\boldsymbol Y_{multi-att} \in \mathbb{R}^{M \times d}$。

注意掩码多头注意力机制的设计和编码器的多头注意力机制是一样的，只是在计算注意力分数时，需要同时使用Padding mask和Look-ahead mask，这样就实现了对目标序列的掩码，下面只介绍俩种掩码机制，其他部分同编码器的多头注意力机制。

Qustion：目标序列的句子长度$M$需要和编码器的句子长度$N$一样吗？
Answer：不需要，因为在transformer中，编码器和译码器是独立的，编码器的输入序列长度$N$和译码器的输入序列长度$M$是可以不一样的，这也是符合人类直觉的，例如中文翻译英文，中文句子长度和英文句子长度是可以不一样的！

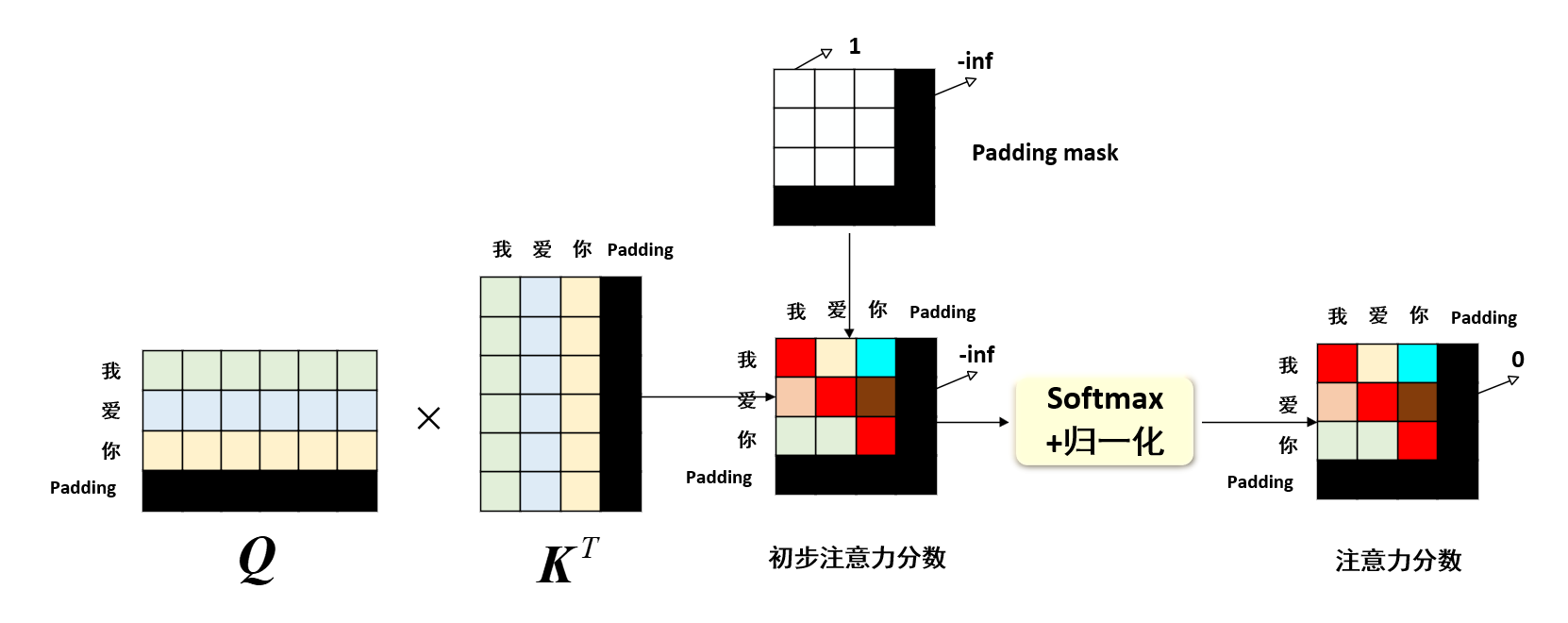
☀️ Padding mask机制

如前所述，我们介绍的例子都是以“我爱中国”这个句子为例，但是在实际应用中，句子的长度是不一样的，例如我们现在需要处理句子“我爱你”，显然这个句子的长度是3，想要批量处理，我们需要对短句子进行padding填充，即将“我爱你”填充为“我爱你[padding]”，这样就可以批量处理了。同样地，对于目标序列“ [start] I love you”，我们也需要对短句子进行padding填充，即将“[start] I love you”可能需要填充为“[start] I love you [padding]”，这样就可以批量处理了。
Qustion：目标序列会不会有标识符[end]呢？
Answer：这个是一个可选项，针对不同的任务，我们可以选择是否加入[end]标识符。在非自回归模型中，我们不需要加入[end]标识符，因为我们是一次性预测所有的目标序列，而在自回归模型中，我们需要加入[end]标识符，因为我们是逐个预测目标序列的每个单词。但是[start]是必须的，这是因为在推理阶段，我们需要一个标识符来告诉模型开始预测目标序列，因为模型是没有标准答案的，模型只能依靠[start]标识符和原始序列特征来开始推理。

然而补充的[padding]是没有意义的，我们不希望模型在注意力机制中关注到这些[padding]，所以我们需要对这些[padding]进行掩码，这就是Padding mask机制，即在计算注意力分数时，将[padding]位置的注意力分数设置为负无穷，这样在softmax后，[padding]位置的注意力分数就会变为0（softmax处理负无穷就会变成0），即模型不会关注到这些[padding]。示意图即如上图。

具体实现过程即：首先针对[padding]设置一个掩码矩阵Padding mask，这个矩阵会在[padding]对应的注意力位置取-inf，其他地方取0，然后在计算注意力分数时，将注意力分数和这个掩码矩阵逐元素相乘，这样就实现了对[padding]的掩码。

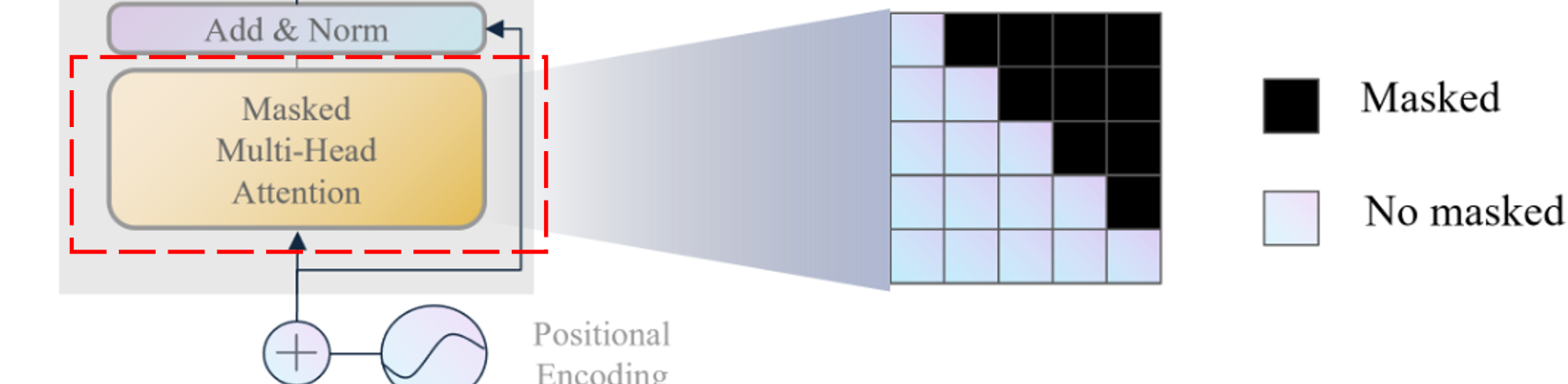
☀️ Look-ahead mask机制（解码器中使用）

当解码器输入目标序列“[start] I love you”时，我们需要让模型逐个预测目标序列的每个单词，即在预测“I”时，模型只能看到“[start]”；在预测“love”时，模型只能看到“[start] I”；在预测“you”时，模型只能看到“[start] I love”，这样就避免了模型提前看到目标序列的问题，这就是Look-ahead mask机制。transformer的具体做法即 避免计算未来的位置的注意力分数，即在计算注意力分数时，将未来位置的注意力分数设置为负无穷，这样在softmax后，未来位置的注意力分数就会变为0，即模型不会关注到未来位置。示意图即如上图。

当然对于解码器，Look-ahead mask机制和Padding mask机制是同时使用的，即在计算注意力分数时，将Padding mask和Look-ahead mask逐元素相乘，这样就实现了对[padding]和未来位置的掩码。

掩码多头注意力机制 程序实现

同编码器的多头注意力机制一样，只是在计算注意力分数时，需要同时使用Padding mask和Look-ahead mask，这样就实现了对目标序列的掩码。

✨交叉注意力机制

• 模块输入：编码器输出：原始序列的上下文特征$\boldsymbol X_{en} \in \mathbb{R}^{N \times d}$和目标序列的上文特征$\boldsymbol Y_{en} \in \mathbb{R}^{M \times d}$。
• 模块输出：交叉注意力机制的输出$\boldsymbol Y_{cross-att} \in \mathbb{R}^{M \times d}$。

我们如何既要结合好原始序列的上下文特征，还要关注现有的目标序列上文特征，从而预测目标序列的下文呢？这就需要使用交叉注意力机制，即在计算注意力分数时，同时使用原始序列的上下文特征和目标序列的上文特征，这样就实现了对原始序列和目标序列的结合，那它具体怎么实现的呢？

还记得多头注意力机制和掩码多头注意力机制中的Q、K、V权值矩阵是怎么获得的吗？编码器是直接将原始序列的嵌入输入$X_{pos}$乘以可学习的$W_Q$，$W_K$，$W_V$得到的，即Q、K、V都只有原始序列特征变换得到。而下图则是交叉注意力机制的做法：

显然，交叉多头注意力机制的V、K矩阵是原始序列特征变换得到的，而Q矩阵是目标序列特征变换得到的，这样就实现了对原始序列和目标序列的结合，这就是交叉注意力机制的设计。为什么呢？

这时候我们就要理解一下transformer设计师为什么叫他们Query、Key、Value了，Query意为查询，Key意为键，Value意为值，这三个矩阵的作用就是这样的，Query是用来查询与Key的相似度，Key是用来被查询的，Value是根据相似度进行加权求出目标值的。因此实质上我们是要翻译原始序列（中文），让它变成目标序列（英文），因此我们需要将Value设置为中文的特征，想把他变成英文。此外，transformer想要根据现有的英文信息去查询中文信息，所以Query设置为英文特征，Key设置为中文特征，用英文查询中文。

笔者觉得一个可能更加有意义的做法：即用原始序列生成Query和value，让目标序列生成Key。这样的做法更加符合人类的思维。在我们人类思维里，比如有一道翻译题，中文是“我爱你”，英文只提供了“I”，需要我们预测后面的单词，显然我需要根据下一个单词“爱”去找对应的英文翻译，即我需要用中文的“爱”去查询英文的“love”，所以我觉得应该将中文特征设置为Query，英文特征设置为Key，用中文查询英文。这样的做法更加符合人类的思维，也更加有意义。

此时你可能恍然大悟，但是还有一个问题没有解决：原始序列的上下文特征形状和目标序列上文的形状不匹配，这会导致什么结果？（下图即说明了这个问题，没有画多头注意力，因为多头只会把最终形状变为$M \times d_k$，经过concat，最终形状还是$M \times d$）

答案是：注意力机制的输出仅和Value形状有关，即最终的输出形状是和Value的形状一样的，因为Key和Query只是为了获得一个注意力分数，而这个注意力分数只是value的权重，不会改变value的形状。因此，我们可以将原始序列的上下文特征和目标序列的上文特征拼接在一起，然后通过线性变换得到Q、K、V，最后通过多头注意力机制得到交叉注意力机制的输出。

交叉注意力机制 程序实现

实现程序同多头注意力机制，只是输入的Q、K、V矩阵不同，这里的Q需要输入目标序列的上文特征，K和V需要输入原始序列的上下文特征。

完整译码层 程序实现

class EncodeLayer(nn.Module):
    def __init__(self, d_model, num_heads=8, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads

        self.layer_norm = LayerNorm(d_model)
        self.multi_attention = MultiheadAttention(d_model, num_heads)
        self.ff_layer = FeedForward(d_model)

        self.dropout = nn.Dropout(p=dropout)

    def forward(self, x):
        _x = x  # 先存储输入，用于后面和attention输出进行残差连接
        x = self.layer_norm(x)  # 输入到attention之前新进行层归一化
        x = self.dropout(self.multi_attention(query=x, key=x, value=x))  # attention 输出
        __x = x  # 存储attention的输出， 用于后面和feedforward的输出残差连接
        x = self.layer_norm(_x + x)  # 对 add之后的结果 norm
        x = self.dropout(self.ff_layer(x))  # feedforward 输出
        x = __x + x  # 残差连接

        return x
        
# 测试代码
# d_model = 512
# x = torch.randn(64, 10, 512)
# encode_layer = EncodeLayer(d_model)
# output = encode_layer(x)
# print(output.shape)  # torch.Size([64, 10, 512])       

完整译码器模块 程序实现

class Encode(nn.Module):
    def __init__(self, d_model, vocab_size=2000,  num_encode_layer=6, num_heads=8, dropout=0.1):
        super().__init__()

        self.vocab_size = vocab_size
        self.d_model = d_model
        self.num_encode_layer = num_encode_layer
        self.num_heads = num_heads
        self.dropout = dropout

        self.embed = nn.Embedding(vocab_size, d_model)  # 定义词典大小

        self.position_encode = PositionalEncoder(d_model)
        self.encode_layer = EncodeLayer(d_model)

        # 六个EncodeLayer层
        self.encode_layers = nn.ModuleList([copy.deepcopy(self.encode_layer) for i in range(num_encode_layer)])

        self.layer_norm = LayerNorm(d_model)

    def forward(self, src):
        x = self.embed(src)
        x = self.position_encode(x)

        # 六个EncodeLayer层依次输出
        for i in range(self.num_encode_layer):
            x = self.encode_layers[i](x)

        return self.layer_norm(x)


# 测试代码
d_model = 512
x = torch.LongTensor([[1, 2, 4]])  # 输入是形状为： [batch_size, seq_length]， 这里batch_zie = 1, seq_len = 3
encode = Encode(d_model=d_model)
output = encode(x)
print(output.shape)  # torch.Size([1, 3, 512])

⭐Transformer实现

import torch
import torch.nn as nn
import torch.nn.functional as F
import math
import copy
import numpy as np

class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len=5000, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.max_seq_len = max_seq_len
        self.dropout = nn.Dropout(p=dropout)

        # 初始化位置编码矩阵
        pe = torch.zeros(max_seq_len, d_model)

        # 计算位置编码
        for pos in range(max_seq_len):
            for i in range(d_model // 2):
                pe[pos, 2 * i] = math.sin(pos / 10000 ** ((2 * i) / d_model))
                pe[pos, 2 * i + 1] = math.cos(pos / 10000 ** ((2 * i) / d_model))

        # 增加 batch_size 维度
        pe = pe.unsqueeze(0)

        # 将pe加入模型，但是不进行更新
        self.register_buffer('pe', pe)

    def forward(self, x):
        seq_len = x.size(1)

        return self.dropout(x + self.pe[:, :seq_len, :])
        
class MultiheadAttention(nn.Module):
    def __init__(self, d_model, num_heads=8, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_k = d_model // num_heads

        # W_Q, W_K, W_V
        self.q_linear = nn.Linear(d_model, d_model)
        self.k_linear = nn.Linear(d_model, d_model)
        self.v_linear = nn.Linear(d_model, d_model)

        self.dropout = nn.Dropout(p=dropout)

        # W_O
        self.out_linear = nn.Linear(d_model, d_model)

    def forward(self, query, key, value, mask=None):
        batch_size = key.size(0)

        # 对输入进行线性变换得到Q, K, V, 然后按头数拆分，最后调整成形状[batch_size, num_heads, seq_len, d_k]
        # 目的就是为了后续计算过程中，各个head之间的独立计算，具体可参考上面详细例子示意
        q = self.q_linear(query).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        k = self.k_linear(key).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        v = self.v_linear(value).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

        scores = torch.matmul(q, k.transpose(-2, -1) / math.sqrt(self.d_k))

        if mask is not None:  # mask 是为了在decode过程中用
            mask = mask.unsqueeze(1)  # 增加一个head维度
            scores = scores.masked_fill(mask == 0, float('-inf'))

        scores = F.softmax(scores, dim=-1)  # -1代表最后一个维度，这里就是为了表示对每一行的元素进行操作

        # 这里实现的就是多个head输出后，然后concatenation
        attention_output = torch.matmul(scores, v).transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)

        # 线性变换得到最后输出
        output = self.out_linear(attention_output)

        return output        

class LayerNorm(nn.Module):
    def __init__(self, d_model, eps=1e-6):
        super().__init__()

        self.gamma = nn.Parameter(torch.ones(d_model))
        self.beta = nn.Parameter(torch.zeros(d_model))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)  # -1代表最后一个维度，对每一行元素进行操作
        var = x.var(-1, keepdim=True) # -1代表最后一个维度，对每一行元素进行操作

        return self.gamma * (x - mean) / torch.sqrt(var + self.eps) + self.beta
        
class FeedForward(nn.Module):
    def __init__(self, d_model, hidden_size=2048, dropout=0.1):
        super().__init__()

        self.linear1 = nn.Linear(d_model, hidden_size)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(p=dropout)
        self.linear2 = nn.Linear(hidden_size, d_model)

    def forward(self, x):
        x = self.linear1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.linear2(x)

        return x


class EncodeLayer(nn.Module):
    def __init__(self, d_model, num_heads=8, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads

        self.layer_norm = LayerNorm(d_model)
        self.multi_attention = MultiheadAttention(d_model, num_heads)
        self.ff_layer = FeedForward(d_model)

        self.dropout = nn.Dropout(p=dropout)

    def forward(self, x):
        _x = x  # 先存储输入，用于后面和attention输出进行残差连接
        x = self.layer_norm(x)  # 输入到attention之前新进行层归一化
        x = self.dropout(self.multi_attention(query=x, key=x, value=x))  # attention 输出
        __x = x  # 存储attention的输出， 用于后面和feedforward的输出残差连接
        x = self.layer_norm(_x + x)  # 对 add之后的结果 norm
        x = self.dropout(self.ff_layer(x))  # feedforward 输出
        x = __x + x  # 残差连接

        return x


class Encode(nn.Module):
    def __init__(self, d_model, vocab_size=2000,  num_encode_layer=6, num_heads=8, dropout=0.1):
        super().__init__()

        self.vocab_size = vocab_size
        self.d_model = d_model
        self.num_encode_layer = num_encode_layer
        self.num_heads = num_heads
        self.dropout = dropout

        self.embed = nn.Embedding(vocab_size, d_model)  # 定义词典大小

        self.position_encode = PositionalEncoder(d_model)
        self.encode_layer = EncodeLayer(d_model)

        # 六个EncodeLayer层
        self.encode_layers = nn.ModuleList([copy.deepcopy(self.encode_layer) for i in range(num_encode_layer)])

        self.layer_norm = LayerNorm(d_model)

    def forward(self, src):
        x = self.embed(src)
        x = self.position_encode(x)

        # 六个EncodeLayer层依次输出
        for i in range(self.num_encode_layer):
            x = self.encode_layers[i](x)

        return self.layer_norm(x)


class DecodeLayer(nn.Module):
    def __init__(self, d_model, dropout=0.1):
        super().__init__()
        self.layer_norm = LayerNorm(d_model)

        self.dropout = nn.Dropout(p=dropout)

        self.multi_attention = MultiheadAttention(d_model)

        self.ff_layer = FeedForward(d_model)

    def forward(self, x, encode_output, trg_mask):
        _x = x                  # 用于掩码多头注意力机制的残差连接
        x = self.layer_norm(x)
        x = _x + self.dropout(self.multi_attention(x, x, x, trg_mask))   # 残差连接
        _x = x                  # 用于编码-解码多头注意力机制的残差连接
        x = self.layer_norm(x)
        x = _x + self.dropout(self.multi_attention(x, encode_output, encode_output)) # 残差连接
        _x = x                  # 用于feedfoward输出的残差连接
        x = self.layer_norm(x)
        x = _x + self.dropout(self.ff_layer(x))

        return x
        
class Decode(nn.Module):
    def __init__(self, d_model, vocab_size=2000, num_decode_layer=6, num_heads=8, dropout=0.1):
        super().__init__()
        self.num_decode_layer = num_decode_layer
        self.embed = nn.Embedding(vocab_size, d_model)

        self.position_encode = PositionalEncoder(d_model)

        self.decode_layer = DecodeLayer(d_model)

        self.decode_layers = nn.ModuleList([copy.deepcopy(self.decode_layer) for i in range(num_decode_layer)])

        self.layer_norm = LayerNorm(d_model)

    def forward(self, trg, encode_output, trg_mask):
        x = self.embed(trg)
        x = self.position_encode(x)
        for i in range(self.num_decode_layer):
            x = self.decode_layers[i](x, encode_output, trg_mask)

        return self.layer_norm(x)
        
def create_mask(size):
    # size: the sequence length of input
    np_mask = np.triu(np.ones((1, size, size)), k=1).astype('uint8')
    trg_mask = torch.from_numpy(np_mask == 0)
    return trg_mask        

if __name__ == "__main__":
    trg_mask = create_mask(size=50)  # size = sequence length

    d_model = 512
    input_encode = torch.randint(1, 5, (64, 50))  # 输入是形状为： [batch_size, seq_length]
    input_decode = torch.randint(1, 5, (64, 50))

    encode = Encode(d_model=d_model)
    encode_output = encode(input_encode)

    decode = Decode(d_model=d_model)
    output = decode(input_decode, encode_output=encode_output, trg_mask=trg_mask)

    print(output.shape)  # torch.Size([64, 50, 512])

后续你就可以使用transformer模型进行各种下游任务了，后面的什么linener层、分类器层、损失函数等等，都是一样的，这里就不再赘述了。