我们在选择损失函数的时候，经常会遇到这样的问题，是选择二元交叉熵（Binary Cross Entropy，BCE），还是选择交叉熵（Cross Entropy，CE）？或许有人简单的认为，二分类问题选择BCE，多分类问题选择CE。那是不是BCE就只能用于二分类问题呢？那么到底有什么细节需要注意呢？本文将为你一一解答。

读完本文你将明白如下：

  • BCE不仅适用于二分类问题，还适用于多标签问题；
  • CE是不会注意负标签的损失的，而BCE会计算负标签的损失；（BCE不是简单的二元CE）
  • BCE 和 CE 在torch中计算log的底数取e，即ln；
  • CE 在torch中输入接收为logits，而BCE接收为概率值；
  • BCE 和 CE 在torch中还有一个参数reduction，用于控制损失的计算方式；
  • CE 在torch接受的标签是向量而不是矩阵。

⭐二分类、多分类、多标签

二分类问题

在正式描述 BCE 和 CE 之前，我们先来了解一下二分类、多分类和多标签的概念。

二分类任务很简单，就是将输入图片分成俩类，即True 和 False。比如，判断一张图片是否是人，模型认为是人，则输出接近于1；模型认为不是人，则输出接近于0。其示意图如下：

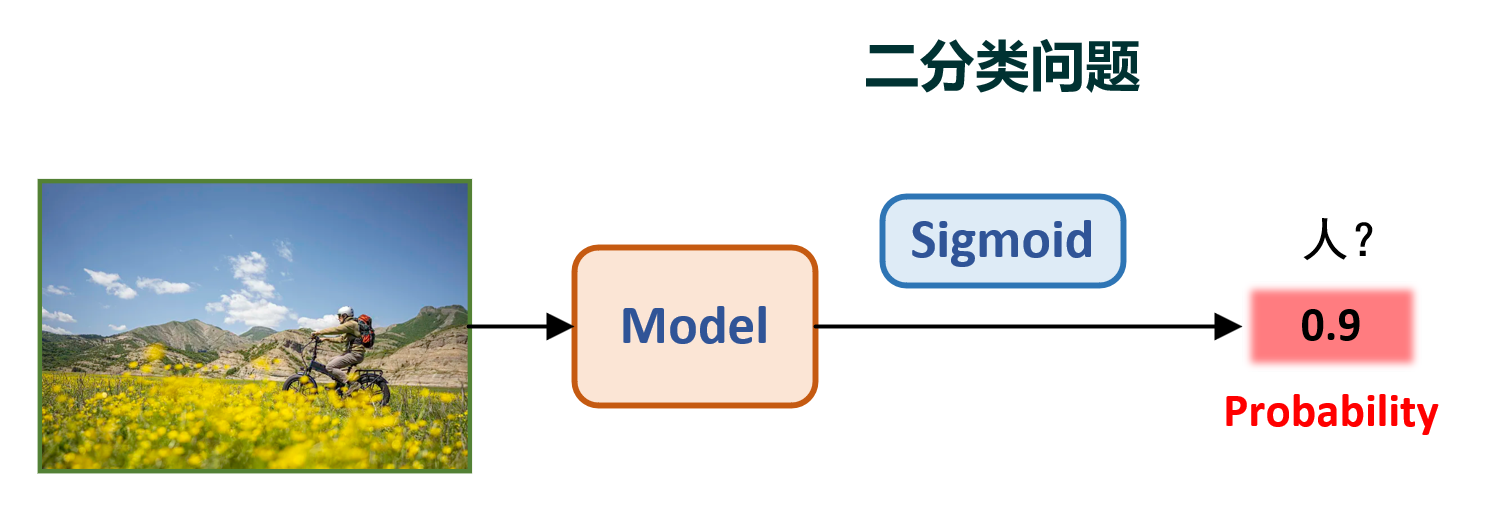
上图中的sigmoid是指将模型输出的原始预测值转换为概率值，sigmoid的作用是让模型的输出值在0-1之间。这样就可以将模型的输出值解释为概率值，即模型认为这张图片是人的概率是多少。

多分类问题

那么如果我还想让模型多输出几个类别呢？，例如需要识别图片是猫，是狗，是鸟，还是人呢？，但是你要注意，多分类任务的前提条件是：每个样本只能属于一个类别。即这个图片如果是猫，那么就不可能是狗、鸟或人。其示意图如下：

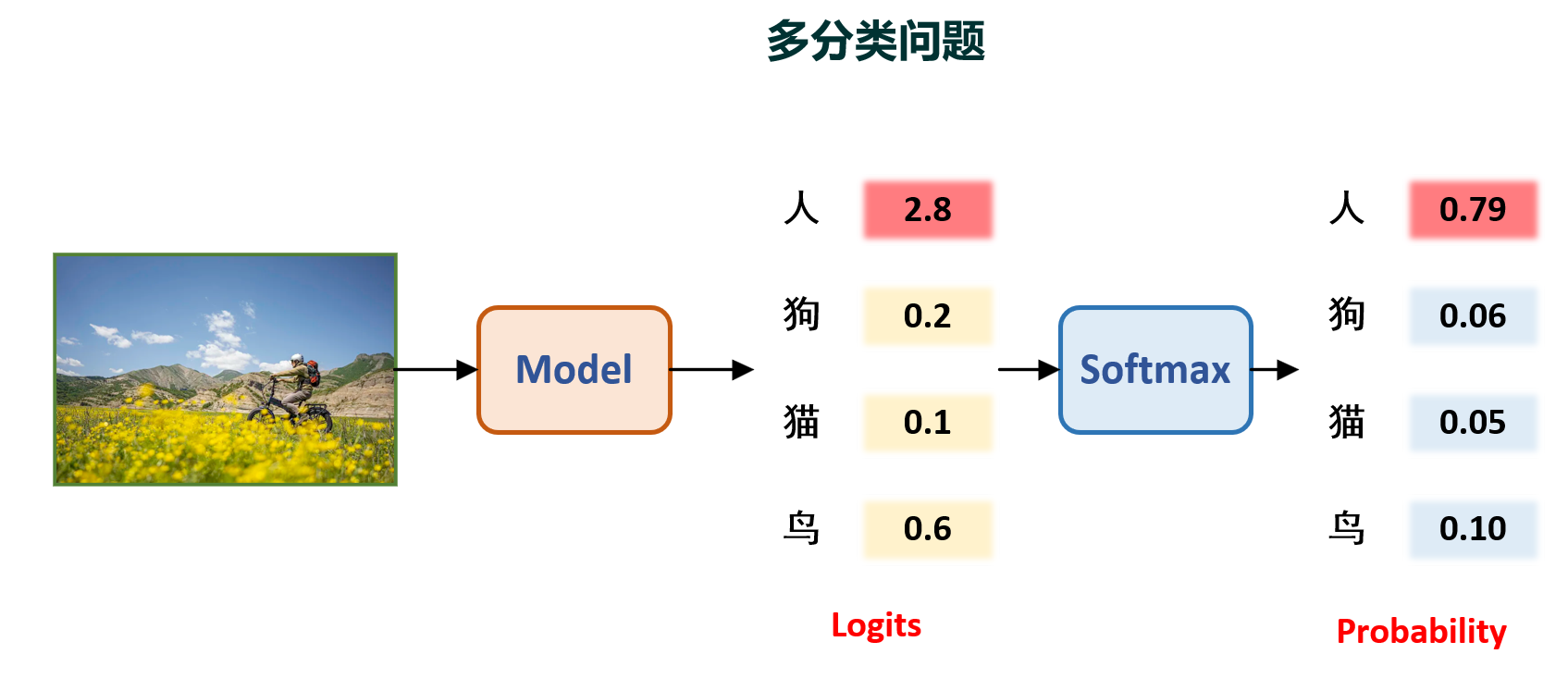
上图中的logits是指模型输出的原始预测值，softmax是指将logits转换为概率值，softmax的作用是让模型的输出值在0-1之间，且所有输出值的和为1。这样就可以将模型的输出值解释为概率值，即模型认为这张图片是猫的概率是多少，是狗的概率是多少，是鸟的概率是多少，是人的概率是多少。

多标签问题

那你显然就会疑惑了，如果我想让模型同时输出多个类别呢？比如，一张图片可能包含多种类别呢？例如一张人的照片背景可能有蓝天、花朵，那么这张图片就是人、蓝天、花朵的多标签任务。其示意图如下：

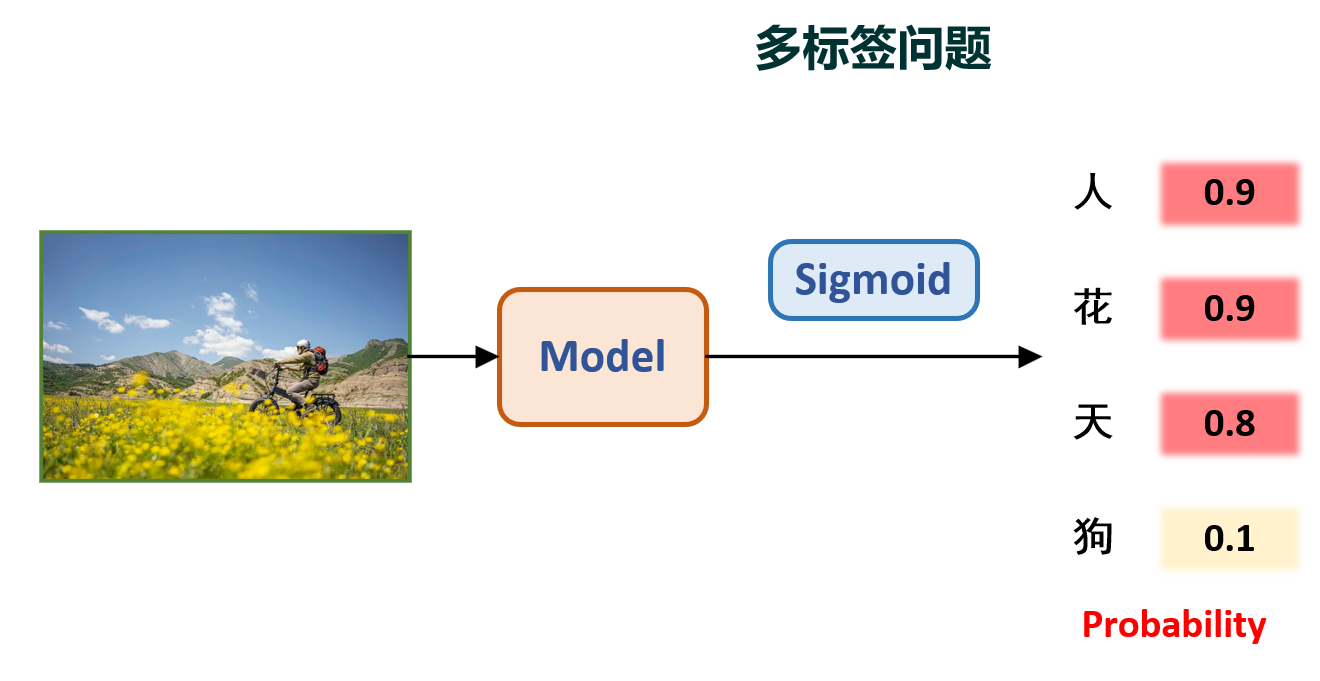
数学描述

我们考虑批量的数据输入，假设有N个样本，每个样本有C个类别。对于二分类问题，每个样本只有一个标签，所以C=1；对于多分类问题，每个样本有多个标签，所以C>1。对于多标签问题，每个样本有多个标签，所以C>1。

模型的输入图片即批量图片$\boldsymbol{X} \in \mathbb{R}^{N \times H \times W}$，对于二分类问题，模型会预测出每个样本的概率值$\boldsymbol{\hat y} \in \mathbb{R}^{N}$，其中$\hat{y_i} \in [0, 1]$。训练的标签即为label$\boldsymbol y \in \mathbb{R}^{N}$，其中$y_i \in \{0, 1\}$。

对于多分类问题，模型会首先预测出不同类别的原始打分logits$\boldsymbol L \in \mathbb{R}^{N \times C}$，然后通过softmax函数将logits转换为概率值$\boldsymbol{\hat Y} \in \mathbb{R}^{N \times C}$，其中$\hat{y_{ij}} \in [0, 1]$。值得注意的是：多分类问题的标签（label）是one-hot编码的。训练的标签即为label$\boldsymbol Y \in \mathbb{R}^{N \times C}$，其中$y_{ij} \in \{0, 1\}$。其中只有一个标签为1，其他标签为0。

对于多标签问题，模型会预测出每个样本的概率值$\boldsymbol{\hat Y} \in \mathbb{R}^{N \times C}$，其中$\hat{y_{ij}} \in [0, 1]$。值得注意的是：多标签问题的标签（label）是多热编码的。训练的标签即为label$\boldsymbol Y \in \mathbb{R}^{N \times C}$，其中$y_{ij} \in \{0, 1\}$。其中可能有多个标签为1，也可能没有标签为1。

⭐BCE 和 CE

二元交叉熵（Binary Cross Entropy，BCE）

对于二分类问题，对于模型的预测$\boldsymbol{\hat y} \in \mathbb{R}^{N}$和标签$\boldsymbol y \in \mathbb{R}^{N}$，我们可以使用二元交叉熵（Binary Cross Entropy，BCE）来计算损失。BCE的数学表达式如下：

显然，当标签$y_i=1$时，第一项为0，第二项为$-\log(1-\hat y_i)$；模型会鼓励模型的输出值$\hat y_i$尽可能的接近1。当标签$y_i=0$时，第一项为$-\log(\hat y_i)$，第二项为0；模型会鼓励模型的输出值$\hat y_i$尽可能的接近0。这样就促使模型预测更接近于标签。且损失的第一项用于计算正标签的损失，第二项用于计算负标签的损失。

显然这里假设的是BCE的输入预测值$\boldsymbol{\hat y}$是一个向量，且每个元素的经过sigmoid函数转换后的概率值。即$\hat y_i \in [0, 1]$。因此记得你设计模型时，最后一层的预测值需要经过sigmoid函数。
此外BCE的输入是可以是矩阵的，这个在多标签问题中会提及。

交叉熵（Cross Entropy，CE）

显然，把问题推广到多分类问题中，模型的预测便是一个矩阵即$\boldsymbol{\hat Y} \in \mathbb{R}^{N \times C}$，标签也是一个矩阵即$\boldsymbol Y \in \mathbb{R}^{N \times C}$。注意这里标签是one-hot编码的。我们可以使用交叉熵（Cross Entropy，CE）来计算损失。CE的数学表达式如下：

我们还可以得到这个公式可以简化为：

其中$y_{i+}$表示第$i$个样本中众多$C$个类别中的正标签的索引，而$\hat y_{i+}$表示模型预测这个正标签类别得到的预测概率值。这样就可以看出，CE是不会注意负标签的损失的，只会计算正标签的损失。
其证明过程如下：由于标签是one-hot编码的，所以$y_{ij} \in \{0, 1\}$，所以当$y_{ij}=0$时，$\log(\hat y_{ij})=0$，所以不会对损失产生影响。
因此对于每一个样本，$C$个类别中只有一个类别是正标签，我们将其索引记为$i+$，即$y_{i+}=1$，而其对应的模型预测值为$\hat y_{i+}$。这样就可以得到：

以上是理论中的CE计算方法，它只会关注正标签的损失，而不会关注负标签的损失。但是在实际中，且计算的$\boldsymbol{\hat Y}$是经过softmax函数转换后的概率值，所以$\hat y_{ij} \in [0, 1]$且$\sum_{j=1}^{C} \hat y_{ij}=1$。然而torch实现的CE有所区别，它是按照logits计算的，这个后续我们会介绍。

矩阵形式的BCE（多标签问题）

显然CE有一个严重缺陷：它默认了每个样本只有一个标签。但是在实际中，我们可能会遇到多标签问题，即每个样本可能有多个标签。这时我们可以使用矩阵形式的BCE来计算损失。对于多标签问题，模型的预测即$\boldsymbol{\hat Y} \in \mathbb{R}^{N \times C}$，标签即$\boldsymbol Y \in \mathbb{R}^{N \times C}$。注意这里标签是多热编码的。我们可以使用矩阵形式的BCE来计算损失。BCE在面对矩阵形式的标签时，数学表达式如下：

显然，它和CE明显的区别是其在计算每个类别时，即考虑了正标签的损失，也考虑了负标签的损失。这样就可以促使模型预测的概率值既接近于正标签，又远离负标签，且其可以要求模型预测多个标签。且当$C=1$时，BCE就退化为二分类问题的BCE。

⭐torch中的BCE和CE

BCELoss的torch介绍

在torch中，BCEloss可以直接调用torch.nn.functional.binary_cross_entropy函数来计算。正常情况下，它的接收常用参数有三个：input、target和reduction。其函数原型如下：

1
torch.nn.functional.binary_cross_entropy(input, target, weight=None, size_average=None, reduce=None, reduction='mean')

其中input是模型的预测值(概率值)，target是标签值，reduction是用于控制损失的计算方式。reduction有三种方式：

  • none：不进行任何计算，直接返回每个样本每个标签的损失值；
  • mean：对每个样本的损失值求均值；
  • sum：对每个样本的损失值求和。

注意有如下要点：

  • BCELoss的input是概率值，即$\hat y_i \in [0, 1]$，因此模型输出需要被sigmoid函数转换；
  • BCELoss的input和target都是矩阵,也可以是向量，计算方法同理论。
  • BCELoss的input和target的数据类型是float。
  • BCELoss的target是多热编码的。
  • BCELoss的reduction默认是mean。
  • BCELoss的对数计算使用的是自然对数ln而不是log!!!。

手撕BCELoss

以多标签问题为例，我们假设样本数量为$N=2$，类别数量为$C=3$。模型预测数据如下：

我们可以直接调用torch.nn.functional.binary_cross_entropy函数来计算损失值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch
import torch.nn.functional as F

# 模型预测值
input = torch.tensor([[1.0, 0.0, 0.8], [0.1, 1.0, 1.0]]).float()
# 标签值
target = torch.tensor([[1, 0, 1], [0, 1, 1]]).float()

# 分别计算三种reduction的损失值
loss_none = F.binary_cross_entropy(input, target, reduction='none')
loss_mean = F.binary_cross_entropy(input, target, reduction='mean')
loss_sum = F.binary_cross_entropy(input, target, reduction='sum')

print('loss_none:', loss_none)
print('loss_mean:', loss_mean)
print('loss_sum:', loss_sum)

编译输出如下：
1
2
3
4
loss_none: tensor([[-0.0000, 0.0000, 0.2231],
        [0.1054, -0.0000, -0.0000]])
loss_mean: tensor(0.0548)
loss_sum: tensor(0.3285)

让我们手算一下验证一下：

  • 当reduction='none'时，损失计算即不进行取均值操作，也不进行求和操作，而是对6个元素分别计算损失值，计算公式即：

    我们即可以逐个计算6个损失：

    所以loss_none的值即为[[0.0, 0.0, 0.2231], [0.1054, 0.0, 0.0]]。

  • 当reduction='mean'时，损失计算即对6个元素求均值，即：

    我们即可以计算：

    所以loss_mean的值即为0.0548。

  • 当reduction='sum'时，损失计算即对6个元素求和，即：

    我们即可以计算：

    所以loss_sum的值即为0.3285。

CELoss的torch介绍

在torch中，CELoss可以直接调用torch.nn.functional.cross_entropy函数来计算。正常情况下，它的接收常用参数有三个：input、target和reduction。其函数原型如下：

1
torch.nn.functional.cross_entropy(input, target, weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

其中input是模型的预测值(logits)，target是标签值，reduction是用于控制损失的计算方式。reduction有同样三种方式。

注意有如下要点：

  • CELoss的input是logits，即$\hat y_{ij} \in (-\infty, +\infty)$，因此模型输出不需要被softmax函数转换；
  • CELoss 会自动对input进行softmax操作；
  • CELoss的input和是矩阵，但是target是向量。
  • CELoss的input的数据类型是float，target的数据类型是long。
  • CELoss的target不是标签矩阵，而是标签向量，它表示每一个样本正样本的索引。
  • CELoss的reduction默认是mean。
  • CELoss的对数计算使用的是自然对数ln而不是log!!!。

torch中的cross_entropy函数会自动对input进行softmax操作，然后计算交叉熵损失，其中softmax的计算公式如下：

手撕CELoss

以多分类问题为例，我们假设样本数量为$N=2$，类别数量为$C=3$。模型预测数据如下：

因此我们得到正标签所在的标签：

我们可以直接调用torch.nn.functional.cross_entropy函数来计算损失值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import torch
import torch.nn.functional as F

# 模型预测值
input_logits = torch.tensor([[-10, 10, 5], [10, -10, -5]]).float()
# 标签值
target = torch.tensor([1, 0]).long()
# 分别计算三种reduction的损失值
loss_none = F.cross_entropy(input_logits, target, reduction='none')
loss_mean = F.cross_entropy(input_logits, target, reduction='mean')
loss_sum = F.cross_entropy(input_logits, target, reduction='sum')

print('loss_none:', loss_none)
print('loss_mean:', loss_mean)
print('loss_sum:', loss_sum)

编译输出如下：
1
2
3
loss_none: tensor([6.7153e-03, 3.5763e-07])
loss_mean: tensor(0.0034)
loss_sum: tensor(0.0067)

让我们手算一下验证一下：

我们首先对输入的input进行softmax操作，得到每个元素的概率值：

  • 当reduction='none'时，损失计算即不进行取均值操作，也不进行求和操作，而是对2个正类别分别计算损失值，我们通过target可以得到正类别的索引，第一个样本的正类别索引为1，第二个样本的正类别索引为0。我们即可以逐个计算2个损失：

    所以loss_none的值即为[6.7153e^{-3}, 3.5763e^{-7}]。

  • 当reduction='mean'时，损失计算即对2个元素求均值，即：

    所以loss_mean的值即为0.0034。

  • 当reduction='sum'时，损失计算即对2个元素求和，即：

    所以loss_sum的值即为0.0067。

⭐总结

所以在分类任务中，如何选择BCE和CE呢？我们可以根据任务的具体情况来选择：

  • 如果是二分类问题，那么选择BCE；
  • 如果是多分类问题，那么选择CE；
  • 如果是多标签问题，那么选择BCE。

此外在torch中，我们还需要注意，BCELoss的input是概率值，而CELoss的input是logits。因此在设计模型时，需要注意BCE模型最后一层的输出需要经过sigmoid函数，而CE模型最后一层的输出不需要经过softmax函数。还有其他的实现细节，例如数据类型，标签的形式等。

这下再也不愁选择损失函数了吧！